Chapitre 15 Solutionnaire

15.1 Chapitre 1

Solution 1.1

Réponse a).

Solution 1.2

Réponse d).

Solution 1.3

Réponse d).

Solution 1.4

Réponse : Figure 1.1 du livre.

Figure 15.1: Comparaison des formes d’organisation en fonction du degré de spécificité des actifs, k; des coûts de transaction, CT(k).

15.2 Chapitre 2

Solution 2.1

Réponse : Figure 2.1 du livre.

Figure 15.2: Représentation de l’ensemble de production et de la fonction de production.

Solution 2.2

Réponse a)

Solution 2.3

Réponse b)

Solution 2.4

Réponse a)

Solution 2.5

Réponse d)

Solution 2.6

Réponse b)

Solution 2.7

7.1 Réponse : Figure 2.6 du livre.

Figure 15.3: De la fonction de production à la productivité moyenne et à la productivité marginale.

7.2 Réponse : Figure 2.7 du livre.

Figure 15.4: Représentation du progrès technique.

Solution 2.8

Réponse a) et b)

Solution 2.9

Réponse b) et d)

Solution 2.10

Réponse b)

Solution 2.11

Réponse a)

Solution 2.12

Réponse c)

Solution 2.13

Réponse :

Si on multiplie par un même facteur constant \(t\) la quantité de tous les intrants \((tK,tL)\) les rendements d’échelles représentent l’influence sur la quantité produite, \(f(tK,tL)\). Les économies d’échelle correspondent ainsi à la partie décroissante de la courbe de coût moyen de long terme.

Solution 2.14

Réponse a)

Solution 2.15

Réponse :

1. Fonction homogène de degré 1/3 = rendements décroissants
2. Fonction homogène de degré 3/2 = rendements croissants

Solution 2.16

Réponse :

1. graphique d’une isoquante : \(K=\frac{1}{L-1}\)

• \(r=1,w=1\)
  • \(TMST = 1 = ~\text{pente de l'isoquante}~ = \frac{1}{L-1}\)
  • \(L=2, K=1\)
• \(r=2,w=3\)
  • \(L=1+\left(\frac{2}{3}\right)^{\frac{1}{2}}\), \(K=\left(\frac{3}{2}\right)^{\frac{1}{2}}\)
• On substitue du Capital au travail (on diminue le facteur le plus cher).

Solution 2.17

Réponse : Même réponse dans les deux cas.

Cas 1) \(q=K=L\) avec \(CT=2q\) et \(CM=2\). Cas 2) \(q=K=L\) avec \(CT=2q\) et \(CM=2\).

Solution 2.18

Réponse :

• \(PM=\frac{PT}{q}\)
• \(\frac{dPM}{dQ}=0\)
• ou \(\frac{dPT}{dQ}=Pm\)
• donc \(\frac{\left(Pm\times Q-PT\right)}{Q^2}=0\)
• \(Pm=PM\)

Solution 2.19

Réponse : Voir l’exercice intéractif en cliquant ici.

Solution 2.20

Réponse :

1. \(CM(y)=CT/y\)
2. \(Cm(y)=\frac{dCT}{dy}\)
3. \(CVM(y)=CV/y\)
4. \(CFM(y)=CF/y\)

Solution 2.21

Réponse :

• \(L=Q+1\)
• \(K=Q+1\)
• \(CT = 2(Q+1)\)

• \(CM=2+2/Q\)
• \(Cm=2\)

Solution 2.22

Réponse : Voir la figure 2.21 du livre

Solution 2.23

Réponse :

• \(\frac{dCM}{dQ}=0\)

• \(CM = \frac{CT}{Q}\)

• \(\frac{d(CT/Q)}{dQ}=0\)

• \(\frac{\left(Cm\cdot Q-CT\right)}{Q^2}=0\)

• \(Cm=CM\)

15.3 Chapitre 3

Solution 3.1

Réponse : a

Solution 3.2

Réponse : d

Solution 3.3

Réponse : b

Solution 3.4

Réponse : b

Solution 3.5

Réponse : voir la figure 3.9 du livre

Solution 3.6

Réponse : c

Solution 3.7

Réponse : b

Solution 3.8

Réponse : a

Solution 3.9

Réponse : d

Solution 3.10

Réponse : b

Solution 3.11

Réponse : b

Solution 3.12

Réponse : c

Solution 3.13

Réponse : Voir les équations 3.3 à 3.6 du livre.

Solution 3.14

Réponse : voir les figures 3.11 à 3.13 dans le livre.

Solution 3.15

Réponse : c

Solution 3.16

Réponse : a

Solution 3.17

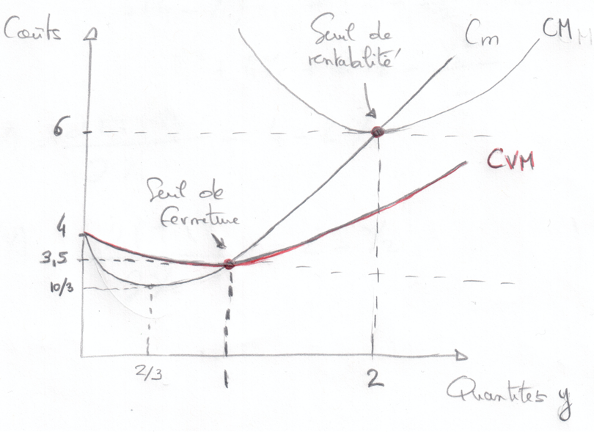
\[CM\left(y\right)=\frac{1}{2}y^2-y+4+\frac{4}{y}\]

\[Cm\left(y\right)=\frac{3}{2}y^2-2y+4\]

\[CVM\left(y\right)=\frac{1}{2}y^2-y+4\]

\[CFM\left(y\right)=\frac{4}{y}\]

Pour tracer ces courbes on va chercher les minimums (conditions de premier ordre).

Solution 3.18

• Pour maximiser les profits en monopole on a \(Rm = Cm\)
• Calculer \(RT\)
• Dériver par rapport à \(Y_1\) et \(Y_2\) pour trouver les \(Rm\)
• Dériver \(CT\) par rapport à \(Y_1\) et \(Y_2\) pour trouver les \(Cm\)
• Égaliser les \(Cm\) et les \(Rm\) pour trouver \(Y_1\) et \(Y_2\) (les quantités)
• En déduire \(p_1, p_2\) et \(\Pi\) (les profits)

Solution 3.19

• À l’équlibre Offre = Demande \(\implies Q_D = Q_O\)
• Résoudre cette équation du 2nd degré (solution : \(P=1,085\))
• En déduire \(Q_D=46\)

• Au nouvel équilibre on aura encore \(Q_D = Q_O\)
• En déduire \(P=5\)
• En déduire \(Q_O=10\)

Solution 3.20

• En CPP on a \(P=Cm\)
• Dériver \(CT\) pour obtenir \(Cm\) (et donc \(P\))
• Inverser l’équation pour avoir \(Q = f(P)\) (la fonction d’offre \(Q_O\))
• Solution \(Q_O = -40 + 10 P\)

• Offre du marché = Offre d’une firme (\(Q_O\)) x le nombre de firme (=20 firmes)

• Offre = demande (\(Q_O = Q_D\))
• En déduire \(P=5\) et \(Q_D=200\)

• Pour maximiser les profits en CPP, il faut trouver \(Q_O\) tel que \(P=Cm\) (Solution \(Q_O=10\))

• \(Π = RT – CT = -5\) (la firme fera des pertes)

Solution 3.21

• Trouver \(CT\) à partir de \(CM\)
• Dériver \(CT\) pour trouver \(Cm\)
• En CPP on aura P=Cm pour maximiser les profits donc \(P = 4q + 6\) et en tournant l’équation \(q = -1,5 + 0,25 P\)
• Offre de marché = offre d’une entreprise x nombre d’entreprises \(\implies Q_O = 100 \times q\)

• \(Q_O = Q_D\)
• \(Q_D = 660 – 2P\) (en tournant l’équation de départ de l’énoncé)
• On en déduit \(P=30\) et \(Q_D=600\)

• En CPP on a \(P=Cm\)
• On en déduit \(q=6\)

• La théorie nous dit que le seuil de rentabilité est au minimum du \(CM + CM =~ ^{CT}/_q\)
• On sait que Cm coupe CM en son minimum
• On aura donc l’égalité CM=Cm, ce qui nous permet d’obtenir \(q=3\)
• Et donc : \(min \{CM\} = 2(3) + 6 + 18/3 = 18\)

• Une firme reste sur un marché si elle est au dessus de son seuil de fermeture (au minimum du \(CV\)). Il faudrait donc \(P > CV\) pour que la firme reste sur le marché.
• \(CVM =~ ^{CV}/_q = 2q + 6\)
• Le minimum du \(CVM\) est au point où \(Cm\) coupe CVM (on trouve donc \(q=0\))
• Et donc : \(min \{CVM\} = 6\)
• \(P=30>6 \implies\) Les firmes restent sur le marché

Solution 3.22

• Trouver \(CT\) (\(=CV +CF\))
• En CPP, \(p=Cm\). Donc, on en déduit \(q=5\) et \(Π =0\)

• Avec \(P=700\) on trouve \(Q_D\)
• Nombre de firmes = \(\frac{Q_D}{q}=102\) firmes

• Seuil de fermeture :
  • Au minimum du \(CVM\), donc au point \(CVM=Cm\)
  • On trouve \(q=0\) et donc un seuil de fermeture lorsque le \(CVM = 600\)
• Seuil de rentabilité :
  • Au minimum du \(CM\), donc au point \(CM=Cm\)
  • On trouve \(CT\) puis \(CM=\frac{CT}{q}\)
  • Même démarche que précédemment (ou alors en faisant les conditions de premier ordre pour CM!)
  • On trouve \(q=5\) et un seuil de rentabilité à \(CM=700\)

Solution 3.23

• \(CT = CV + CF\)
• En monopole, pour maximiser les profits on aura \(Rm = Cm\)
• Trouver \(Cm\) en dérivant \(CT\)
• Inverser la demande de marcher pour obtenir \(P = 1400 – 4Q\)
• \(RT = P x Q\)
• Trouver \(Rm\) en dérivant \(RT\)
• Déduire \(Q=140\) (Avec \(Rm =Cm\))
• Déduire \(P = 840\)

• Pour maximiser le \(CA\) en monopole on aura \(Rm = 0\)
• En déduire \(Q=175\) et \(P=700\)

• En cas de concurrence on aura \(RM = Cm\)
• En déduire \(Q=233\) et \(P=466.8\)

• Avec les conditions calculées en 3) on trouve \(CV\) et \(CVM\)
• On en déduit facilement en regardant ces équations que le minimum de \(CVM\) est quand \(Q=0\)
• L’entreprise ne fermera pas.

Solution 3.24

• \(Rm =Cm\)
• Dériver \(CT\) pour trouver \(Cm\)
• Inverser \(Q = F(P)\) pour trouver \(P = f-1(Q)\)
• Trouver \(RT\) puis dériver pour obtenir \(Rm\)
• Trouver \(Q\) avec l’égalité \(Rm = Cm\)
• En déduire \(P = 750\) et \(Π = 50 000\)

• Le gouvernement impose une situation de CPP où \(P=Cm\)
• En déduire \(Q = 3000\) et \(P = 500\)

15.4 Chapitre 4

Solution 4.1

Calculer d’abord les fonctions de réaction :

• \(Π_1= RT_1 – C_1\)
• \(Π_1= P \times y_1 –C_1\)
• \(Π_1= (4-Y)y_1 – y_2\) Avec \(Y = y_1 + y_2\)

Ensuite on fait la dérivée première de \(Π_1\) par rapport à \(y_1\) On en déduit la fonction de réaction \(y_1 = R_1 (y_2) = -^1/_2 y_2 + ^3/_2\)

Faire la même démarche pour trouver la fonction de réaction de l’entreprise 2. Pour trouver les quantités \(y_1^*\) et \(y_2^*\) on pose: \(y_1 = R_1(y_2) = R_1 (R_2 (y_1))\)

On en déduit \(y_1^* =1\) et \(y_2^* =1\)

Puis \(Y=2, P=2, Π_1 =1 ~\text{et}~ Π_2 =1,5\)

La firme leader (2) fixe son prix en premier en tenant compte de ce que fera la firme suiveuse (1). Elle va ainsi maximiser son profit.

• On sait que ce qui maximise le profit de la firme suiveuse (firme 1) c’est:
  • \(y_1 = R_1 (y_2) = -^1/_2 y_2 + ^3/_2\)
• On insère cette équation dans la fonction \(Π_2\)
• On maximise \(Π_2\) en faisant la dérivée première.
• On trouve \(y_2\).
• On en déduit : \(y_1, P, Π_1, Π_2\)

Solution 4.2

• Idem que dans l’exercice 1. On trouvera \(q_1 = 7,59\) et \(q_2 = 6,96\)

• Idem que dans l’exercice 1. On trouvera \(q_1 = 9,52\) et \(q_2 = 6,19\)

Solution 4.3

• En supposant qu’elle est seule sur le marché (monopole) chaque entreprise assimile la fonction de demande sur le marché à sa fonction de recette moyenne.
  • On supposera donc \(Q=q_1\)
  • On trouve RT1, Rm1 et Cm1
• Pour maximiser son profit, la firme posera la condition \(Rm = Cm\)
  • On trouve \(q_1 = 3\)
• Même démarche pour la firme 2. On trouvera \(q_2 = 12\)
• On en déduit \(P, Π_1 et Π_2\)
• Ici vous trouverez des profits négatifs pour les 2 entreprises. En s’ignorant, les deux firmes feront des pertes.
• Solution : \(P = 250\), \(Profit_1=-10\) et \(Profit_2=-40\)

• Idem que des les exercices 1 et 2.
  • On trouvera \(q_1 = 2\) et \(q_2 = 10\)
  • \(Profit_1=0\) et \(Profit_2 = 100\)
  • La firme 1 fait zéro profit dans ce cas!

Solution 4.4

• Tourner l’équation \(Q= f(P)\) pour avoir plutôt \(P= f-1(Q)\)
• Trouver les fonctions de réaction et en déduire \(q_1, q_2, P, Π_1, Π_2\)
  
• C’est un duopole de COURNOT
• Solution : \(Q1=37\), \(Q2=21\), \(P=84\), \(Profit_1=2738\), \(Profit_2=1323\)

• Si les firmes s’entendent la nouvelle situation d’équilibre sera :
  • \(ΠT = Π1 + Π2\)
• On fait ensuite les dérivées premières de \(Π_T\) par rapport à \(q_1\) et \(q_2\)
  • On égalise les deux dérivées premières (toutes les deux égales à zéro).
• Avec une simplification on arrive avec :
  • \(-4q_2 +190 = - 6q_2 +200\)
• On trouve \(q_2 =5\) et on déduit \(q_1 =42,5\)
• On en déduit \(P, Π_T , Π_1 , Π_2\)
• Solution : \(Q2=5\), \(Q1=42.5\), \(P=105\) et \(Profit_{total}=-4537.5\)

15.5 Chapitre 5

Solution 5.1

Situation dans laquelle l’entreprise en place décide d’une tarification de son produit et dont la conséquence directe est l’éviction des entrants potentiels

Solution 5.2

Lorsqu’une entreprise, généralement dominante, fixe ses prix pendant une période de temps suffisamment longue, à un niveau si bas, qu’un ou plusieurs de ses concurrents doivent quitter le marché ou que d’autres entreprises doivent renoncer à y entrer (verrouillage de marché)

Solution 5.3

1. Déterminer leur objectif prioritaire : maximisation des bénéfices, maximisation du chiffre d’affaires, stratégie de croissance, stratégie de survie, stratégie d’écrémage, valorisation de l’image de marque, etc.
2. Les entreprises doivent mesurer les réactions probables du marché à partir de la courbe de demande et des facteurs affectant la sensibilité au prix
3. Il est indispensable pour les entreprises d’évaluer leurs coûts de fabrication pour différents volumes de production, sans négliger l’influence des économies d’échelle et de l’effet d’expérience
4. Les entreprises doivent aussi étudier les cinq forces concurrentielles.
5. Les entreprises ont à choisir une méthode de tarification telle que la méthode «coût-plus-marge» ou celles du taux de rentabilité souhaité ou de la valeur perçue, ou encore un dosage de plusieurs d’entre elles
6. Les entreprises doivent proposer un prix qui tienne compte de la dimension psychologique de l’acte d’achat, et dans certains cas des directives des pouvoirs publics.

Solution 5.4

Réponse d)

Solution 5.5

1. L’entreprise qui se lance dans une telle politique doit assurer sa crédibilité aux yeux des concurrents.
2. L’entreprise doit être également assurée de sa rentabilité, en ce sens que les dépenses occasionnées par cette politique sont plus que compensées par le supplément de recettes qui en résultent

Excercice 5.6

Un surinvestissant dans des moyens de production.

Excercice 5.7

1. Le présumé prédateur détient-il un pouvoir de marché, autrement dit, a-t-il la capacité d’influencer de façon unilatérale les prix dans le secteur concerné ? Au-delà d’une part de marché fixée par les autorités (au Canada, 35 %), on considère souvent que l’entreprise détient un certain pouvoir de marché. On prend aussi en considération le nombre total de vendeurs et les disparités de taille qui existent entre les vendeurs.

2. Dans le cas où la réponse à la question précédente est positive, on peut alors poser la question suivante : les prix sont-ils déraisonnablement bas ?

15.6 Chapitre 6

Solution 6.1

La discrimination par les prix consiste en la vente de différentes unités d’un bien à des prix différents, soit aux mêmes consommateurs, soit à des consommateurs différents.

Solution 6.2

1. L’entreprise connaît chaque consommateur constituant cette fonction de demande (discrimination au premier degré)
2. L’entreprise peut faire plusieurs groupes sans pouvoir déterminer dans quel groupe un individu donné préfère se trouver (discrimination au deuxième degré)
3. L’entreprise peut faire plusieurs groupes et y classer les individus (discrimination au troisième degré).

Solution 6.3

1. La discrimination au premier degré correspond à une situation où l’entreprise vend les différentes unités d’extrant à des prix différents et où ces prix peuvent différer d’une personne à l’autre.
2. La discrimination au deuxième degré est également appelée «tarification non linéaire» parce qu’elle implique que le prix par unité d’extrant dépend de la quantité achetée.
3. L’entreprise pratique des prix différents selon des groupes qu’elle détermine.

Solution 6.4

Exemple Disney, tarifs des parcs d’attraction, tarifs des compagnies aériennes, etc.

Solution 6.5

1. Une vente liée est une pratique commerciale consistant à lier la vente d’un produit à l’achat d’un autre produit.
2. Les ventes par assortiments représentent des ventes de produits différents vendus sous le même emballage.

Solution 6.6

Solution 6.7

15.7 Chapitre 7

Solution 7.1

Une catégorie générale de produits est différenciée s’il existe une base suffisante pour distinguer les marchandises d’un vendeur de celles d’un autre. Peu importe que cette base soit réelle ou illusoire, aussi longtemps qu’elle revêt une importance quelconque pour les acheteurs, et mène à la préférence d’une variété de produits sur une autre.

Solution 7.2

1. La différenciation horizontale ou spatiale, qui renvoie à des différences de goût subjectives entre les consommateurs (il n’y a pas de caractéristiques objectives du produit)
2. La différenciation verticale, où tous les consommateurs sont d’accord pour classer les produits de la même façon (il y a une perception unanime sur certaines caractéristiques du produit : par exemple, la qualité).

Solution 7.3

La différenciation correspond à une distance physique : la distance qui sépare les consommateurs de chacune des entreprises. Les consommateurs sont localisés en des points différents et payent des coûts de transport qui dépendent de la distance qu’ils doivent parcourir lorsqu’ils vont acheter un produit.

Solution 7.4

Hotteling

Solution 7.5

1. Pour des prix fixés et des coûts de transport linéaires, les deux entreprises se localisent à l’équilibre au milieu de la ville (différenciation minimale). Chaque entreprise se localise à cet endroit, car en l’absence de concurrence par les prix, elle cherche à avoir le maximum de parts de marché.

2. si les entreprises sont chacune à un bout du segment \(a=0\) et \(b=1\), alors les prix sont élevés. Les entreprises font de la différenciation maximale et l’effet de concurrence est diminué, mais les parts de marché baissent à cause des prix élevés. On appelle cet effet l’«effet centrifuge». Les entreprises s’éloignent en vue de constituer des monopoles locaux qui atténuent la concurrence en prix qu’elles se livrent.

Solution 7.6

Solution 7.7

Solution 7.8

1. Les consommateurs sont situés sur un cercle de circonférence égale à 1, de façon uniforme. Dans ce cas, l’espace produit est totalement homogène (aucune localisation n’est à priori meilleure qu’une autre). Tous les déplacements se font le long du cercle (imaginons des supermarchés dans une banlieue circulaire, la ville étant coûteuse à traverser)

2. Le principe de différentiation maximale s’applique

Solution 7.9

La différenciation verticale tient compte de la qualité des produits. Dans ce cas et à l’encontre de la différenciation horizontale, tous les consommateurs ont les mêmes préférences pour le produit. Ils sont tous d’accord pour dire qu’un produit est de meilleure qualité, c’est-à-dire que sa distance psychologique par rapport à d’autres produits de moins bonne qualité est moindre. La qualité d’un produit est donc une variable stratégique.

15.8 Chapitre 8

Solution 8.1

1. L’innovation en continu
2. L’innovation technologique vs organisationnelle
3. L’innovation concurentielle

Solution 8.2

1. Les dépenses en RD sont plus généralement conduites par de grandes entreprises;
2. Les dépenses en RD sont plus généralement conduites dans des industries où les entreprises ont naturellement des parts de marché importantes, c’est-à-dire des industries à structure oligopolistique.

Solution 8.3

1. Dans un marché concurrentiel, une entreprise n’innove que si le coût de l’innovation est inférieur à l’augmentation de profit provenant de l’innovation
2. Si l’innovation n’est pas transférable, alors l’entreprise aura un intérêt à investir afin de diminuer sa fonction de coût en raison de l’innovation et de tarifer à un prix inférieur à toutes les autres entreprises, se retrouvant en situation de monopole
3. Une entreprise en situation de monopole accordera moins de valeur à une innovation qu’une entreprise en situation de concurrence, la première entreprise faisant déjà un profit de monopole (Les entreprises font moins de R&D que ce qu’elles devraient).

Solution 8.4

Plus le secteur est concurrentiel et plus les investissements en R&D sont faibles.

Solution 8.5

1. La première porte sur la sensibilité au point de départ, mais où il n’y a pas de sous-optimalité. Par exemple, le langage, ou les conventions telles que conduire une voiture du côté droit de la route. Conduire à gauche ne serait pas sous-optimal, ce serait juste une autre forme de convention

2. La deuxième catégorie porte aussi sur la sensibilité au point de départ, mais avec une sous-optimalité ex post, mais pas de sous-optimalité au moment de l’innovation : aucune meilleure décision n’était possible. C’est l’exemple du clavier QWERTY.

3. La troisième catégorie porte aussi sur la sensibilité au point de départ avec sous-optimalité ex ante et ex post. En d’autres termes, l’innovation choisie comme point de départ est sous-optimale par rapport à ce qui aurait pu être choisi d’un point de vue technologique. Ce sont les exemples du Betacam contre le VHS, de MS-DOS contre Apple contre DR-DOS (le système d’exploitation de Digital Research).

Solution 8.6

Possibilité pour une entreprise de l’«ancienne» économie de voir ses parts de marché se réduire à cause de la réplication de son offre sur un site Internet. Quasiment inexistant auparavant, ce risque a pris de l’ampleur avec Internet.

Exemple : la sortie du iPhone a coïncidé avec la chute des ventes de ses lecteurs de musique iPod. Ce phénomène de cannibalisation s’est amplifié avec la venue de l’iPad en 2011, moment où la compagnie offrait sur le marché trois appareils permettant d’écouter de la musique. De plus, les ventes d’iPad ont fortement impacté la croissance des ventes des ordinateurs personnels iMac dès la moitié de l’année 2012

Solution 8.7

Réponse : Voir l’exercice intéractif en cliquant ici.

15.9 Chapitre 9

Solution 9.1

Groupe d’entreprises ayant accepté explicitement de coordonner leurs activités afin d’augmenter leurs profits.

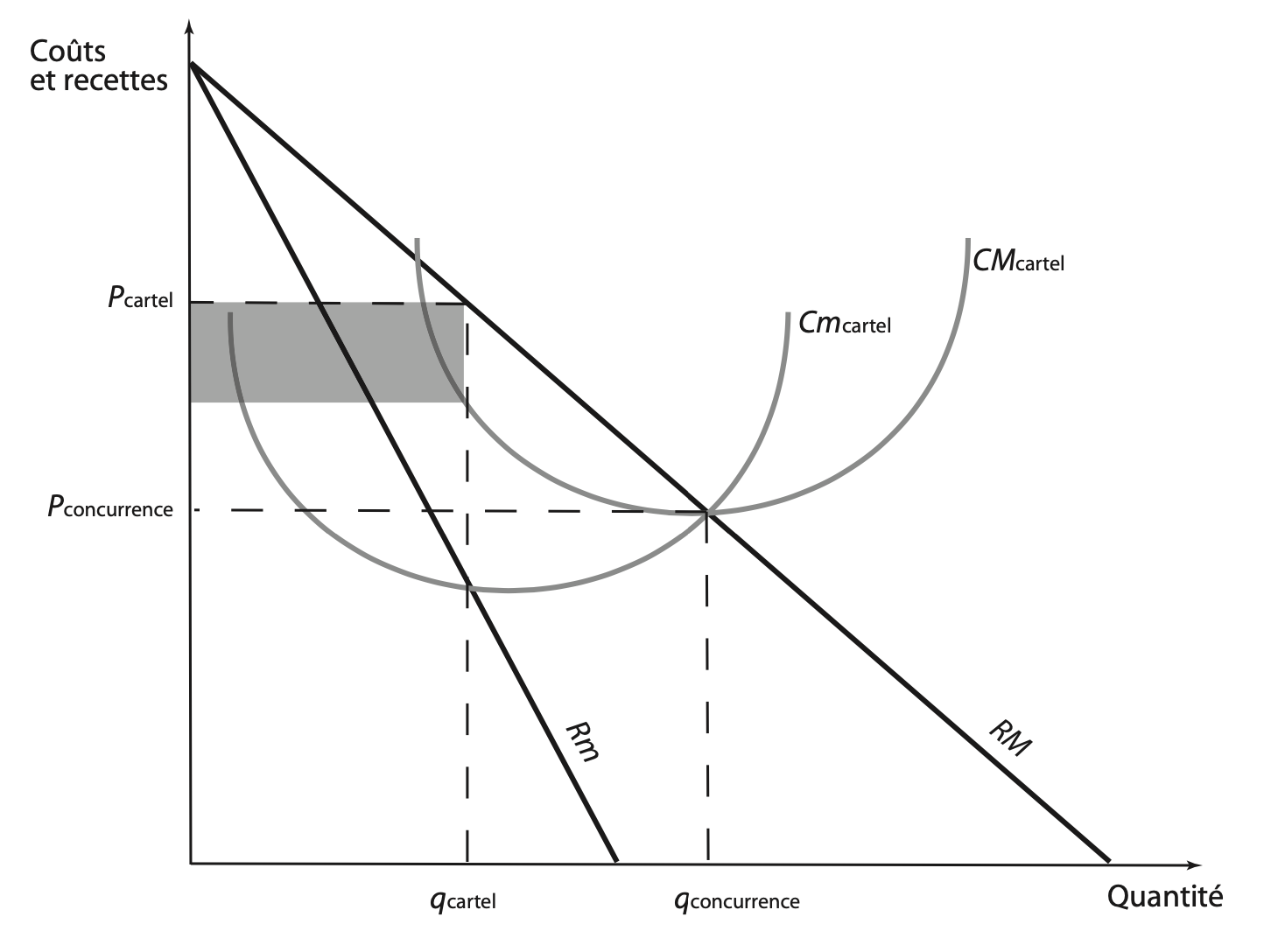
Solution 9.2

Solution 9.3

Une fois que l’équilibre est défini par l’organisme centralisateur, il peut être payant pour une entreprise d’avoir un comportement opportuniste (ou déviant) et de profiter du prix élevé pour vendre une quantité plus importante. Cette attitude frauduleuse peut provoquer une dynamique instable, les autres firmes pouvant adopter la même stratégie. (Incitations à tricher)

Illustration par la théorie des jeux :

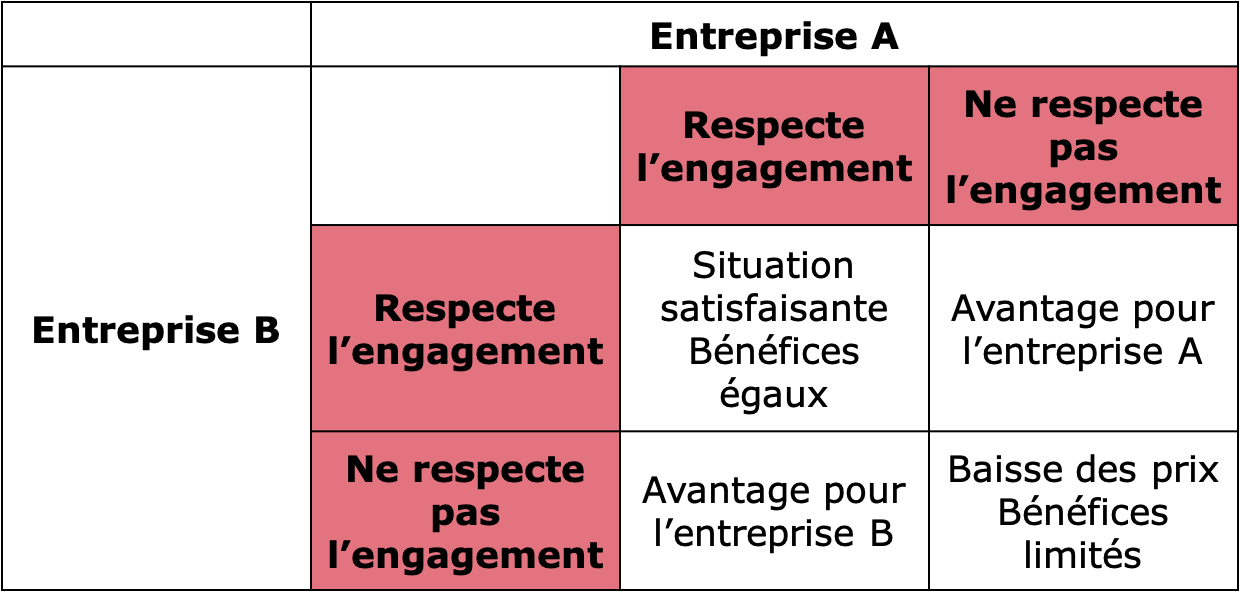
Solution 9.4

1. Aller plus loin que le prix
2. Diviser le marché
3. Déterminer les parts de marché
4. Inclure la clause des «nations les plus favorisées»
5. Inclure la clause «on paye la différence»
6. Les prix de déclenchement

Solution 9.5

1. Quasi-intégration : Relations suivies de marché entre des entreprises indépendantes situées à des stades de production différents
2. L’impartition : l’entreprise «ne doit pas considérer seulement son intérêt à court terme mais, en se plaçant dans une perspective stratégique, doit considérer l’autre comme un partenaire avec lequel il faut s’attacher à développer une collaboration susceptible de produire des effets de synergie où chacun trouve son avantage
3. Les accords de coopération : ’ode de croissance réfléchi et limité dans le temps, qui crée des liens d’interdépendance entre deux ou plusieurs entreprises, concurrentes ou non, sans généralement aboutir à des situations de contrôle juridique fort et direct
4. Les alliances stratégiques : Accord conclu et géré conjointement par plusieurs entreprises concurrentes, ou potentiellement concurrentes, qui choisissent de mener à bien un projet, un programme ou une activité spécifique en coordonnant les compétences, les moyens et les ressources nécessaires
5. Une entreprise commune : Entreprise juridiquement indépendante, généralement créée par deux entreprises, qui en partagent la propriété selon une répartition donnée. Nous avons vu précédemment que les filiales communes pouvaient être qualifiées de coopératives ou de concentratives. Les entreprises communes sont souvent le fait d’entreprises de nationalités différentes

Solution 9.6

(Fusion-acquisition) est “l’opération par laquelle deux ou plusieurs sociétés se réunissent pour n’en former plus qu’une seule, soit par l’absorption d’une ou de plusieurs sociétés par une autre, soit par la réunion des sociétés objets de la fusion dans une société nouvelle créée à cet effet”.

Solution 9.7

1. Les synergies
2. Les barrières à l’entrée et pouvoir de marché

Solution 9.8

1. Motivations purement financières
2. Réaliser « une bonne affaire » ou d’éliminer un concurrent gênant
3. Le goût pour le pouvoir
4. Des dirigeants peu performants qui réduisent la valeur boursière de la firme à tel point qu’il devient profitable pour des firmes concurrentes d’en prendre le contrôle

Solution 9.9

1. La recherche-développement (partage des coûts et des risques)
2. La flexibilité et la réversibilité
3. La volonté de participer à la création d’une norme (d’un « standard »)
4. Se réunir dans le cadre d’un projet commun

15.10 Chapitre 10

Solution 10.1

Mercantilisme

Solution 10.2

La théorie des avantages comparatifs

Solution 10.3

Les hypothèses similaires au modèle néo-classique en général:

1. Aucun coût de mobilité des facteurs au sein des pays ou coût d’ajustement des économies;
2. Aucune mobilité internationale des facteurs de production;
3. Plein emploi des facteurs de production.

Les hypothèses supplémentaires:

1. Des demandes identiques (pour n’avoir qu’un seul ratio de prix relatifs)
2. Rendements d’échelle constants
3. Concurrence pure et parfaite
4. La technologie est identique
5. Les dotations factorielles sont différentes

Solution 10.4

Un pays va exporter le bien qui requiert une utilisation relativement plus intensive du facteur de production relativement abondant, et importera le bien qui requiert une utilisation relativement plus intensive du facteur de production relativement plus rare

15.11 Chapitre 11

Solution 11.1

1. Le courant de Harvard (Courant structuraliste)
2. L’école de Chicago

Solution 11.2

1. La rentabilité supérieure de la grande firme n’est pas le fait d’une domination abusive du marché ou d’un pouvoir de monopole, mais proviendrait d’une efficience supérieure liée notamment à la présence d’économies d’échelle, d’économies de gamme et de possibilités d’apprentissage. Les travaux de Demsetz (1973) montrent que les petites entreprises agissant sur des marchés.

2. Même s’il existait une liaison statistique entre le taux de concentration et la rentabilité, cette liaison doit s’apprécier de manière dynamique et non statique.

Solution 11.3

Sherman Act et du Clayton Act.

15.12 Chapitre 12

Solution 12.1

Négociations de types de produits ou services qui vont pouvoir être échangés, ou qui pourront voir leurs droits de douane diminués ou réduits à zéro.

Solution 12.2

15.13 Chapitre 13

Solution 13.1

Risque : Ensemble d’événements dont la probabilité d’occurrence est connue. La valeur est inconnue mais l’expérience permet de s’en faire une idée, selon Loubergé (1994) : «c’est la valeur vers laquelle tend la fréquence d’un événement au fur et à mesure que le nombre d’expériences augmente ».

Incertitude : Un ensemble d’événements dont la probabilité de survenance n’est pas mesurable.

Solution 13.2

Les agents économiques peuvent estimer subjectivement la vraisemblance d’un événement en fonction de leurs informations

Solution 13.3

Par définition, un modèle ignore certains aspects de la réalité» . Il s’agit d’une surprise. L’incertitude correspond alors à une information sur les événements possibles tout en tenant compte que ces événements ne sont pas les seuls, et qu’il peut s’en produire d’autres, inconnus à ce jour.

Solution 13.4

1. Parfait/imparfaite L’information parfaite (imparfaite) correspond à une situation où le joueur (ne) connaît (pas) sa position dans l’arbre du jeu, en d’autres termes, il (ne) sait (pas) ce que l’autre joueur a joué avant lui dans un jeu séquentiel.

2. Complète/imcomplète L’information complète signifie que l’ensemble des stratégies, des événements et des paiements sont connus.

Solution 13.4

L’incertitude radicale correspond à la possibilité d’occurrence d’événements non-anticipés car ne pouvant pas être identifiées en l’état de la connaissance scientifique du moment. C’est, par exemple, une entreprise qui n’a pas tenu compte dans ses décisions stratégiques de l’introduction sur le marché d’un procédé technologique innovant par une entreprise concurrente.