set.seed(123)
simulate_recovery <- function(T=60, dip=0.5, tmin=10, tmax=40) {
# Pre-shock performance = 1; shock at t=0 reduces to 1-dip; recovery to 1
t <- 0:T
trough <- 1 - dip
t_recover <- sample(tmin:tmax, 1)
q <- rep(1, length(t))
q[1:(t_recover+1)] <- trough + (1 - trough) * (0:t_recover)/t_recover
data.frame(t=t, Q=q)
}
path <- simulate_recovery()
R <- 1 - mean(1 - path$Q) # discrete approx to the area metric
list(resilience_index = round(R, 3))
# $resilience_index
# [1] 0.83214 Resilience of Global Supply Chains in a Geopolitical Age
The global economy relies on intricate supply networks in which firms, logistics platforms, and institutions bridge spatial, regulatory, and informational divides. For three decades, the dominant organizing logic favored lean, globally dispersed architectures, minimizing buffers to exploit economies of scale and comparative advantage. The COVID-19 pandemic, U.S.–China trade frictions, and the war in Ukraine offered unambiguous evidence that such systems are exposed to non-trivial tail risks and policy discontinuities that propagate through production networks in ways that classical firm-level risk frameworks understate. A fundamental lesson emerged: resilience is not a simple attribute of a firm or a facility but an emergent property of a network embedded in legal and geopolitical regimes, where interdependencies, concentration, and coordination frictions shape both shock transmission and recovery trajectories (Acemoglu, Carvalho, Ozdaglar, & Tahbaz-Salehi, 2012; Carvalho, Nirei, Saito, & Tahbaz-Salehi, 2021).
This chapter develops a theoretically grounded and empirically oriented analysis of supply chain resilience under geopolitical risk. The argument synthesizes three analytic lenses. First, complex systems and network theory clarify how topology and dependency structures govern non-linear propagation, critical nodes, and cascading failures in production networks. Second, institutional economics explains how formal rules, credible commitments, and governance arrangements enable or constrain diversification, coordination, and recovery. Third, strategy and operations research illuminate the efficiency–resilience trade-off and the design of mitigation portfolios that combine redundancy, flexibility, visibility, and agility. Throughout, I integrate code snippets to operationalize core constructs: visualizing network vulnerability, quantifying concentration, simulating cascade dynamics, and sketching empirical pipelines for tracking reconfiguration over time. I focus on cross-sectoral insights that hold for semiconductors, pharmaceuticals, food, and energy, while recognizing sectoral idiosyncrasies.
14.1 Conceptual foundations: networks, institutions, and resilience metrics
Production networks are characterized by incomplete contracts, relationship-specific investments, and tiered, multi-country sourcing that amplify the role of coordination, information, and bargaining in determining outcomes (Antràs & Chor, 2013). Network theory formalizes two properties central to resilience. First, centrality identifies suppliers or logistics nodes whose failure disproportionately disrupts system connectivity. Second, modularity and redundancy govern the extent to which shocks can be localized and rerouted rather than globalized through the network. In the macroeconomics of networks, idiosyncratic supplier shocks can generate aggregate fluctuations when the network exhibits sufficient skewness or “granularity,” and their propagation depends on input–output linkages and substitution possibilities (Acemoglu et al., 2012; Carvalho et al., 2021).
Institutional economics highlights how credible rules, dispute resolution, standards, and trade agreements reduce transaction costs and uncertainty, thereby facilitating multi-sourcing and cross-border coordination. Conversely, geopolitical rivalry, sanctions, export controls, and border frictions function as state-contingent shocks that alter relative prices and feasibility constraints, sometimes in highly non-linear ways. The literature on weaponized interdependence demonstrates how nodal chokepoints in global infrastructures and standards enable coercive leverage that firms must treat as a parameter in resilience calculus (Farrell & Newman, 2019).
Operationalizing resilience requires metrics that capture both resistance and recovery. Let \(Q(t)\) denote a normalized performance index for a focal supply chain, scaled to one pre-shock. A common integral measure defines resilience over a horizon \([t_0, t_1]\) as \(R = 1 - \frac{1}{t_1 - t_0}\int_{t_0}^{t_1} [1 - Q(t)] \, dt\). This area-based metric rewards higher performance during disruption and faster recovery, and it is sensitive to both depth and duration of impairment. Complementary indicators include time-to-recovery, time-to-survive, service fill rates, and the expected shortfall given a distribution of shock scenarios. The code below illustrates the computation of a standard area-based resilience index under simulated recovery paths.
The conceptual message is straightforward. Network topology, institutional context, and operational design jointly determine \(Q(t)\). The same exogenous shock can produce distinct \(Q(t)\) paths across firms and sectors because structure and governance differ.
14.2 Geopolitical disruptions and network propagation
Three salient disruptions illustrate the interaction between geopolitics and network structure. First, pandemic lockdowns disrupted manufacturing, ports, and last-mile logistics across multiple hubs, producing simultaneous supply and demand shocks, container misallocations, and non-linear oscillations in lead times. Second, trade tensions and export controls altered the feasibility of cross-border intermediate trade, especially in dual-use technologies, forcing firms to reallocate sourcing and reoptimize tariffs-versus-lead-time trade-offs. Third, the Russia–Ukraine war abruptly constrained energy and agricultural exports, exposed European import dependencies, and generated rerouting and substitution cascades with price and availability effects across multiple tiers. Empirical evidence from the Great East Japan Earthquake shows how geographically localized shocks transmit through input–output linkages and supplier networks to affect distant plants and downstream firms in ways that depend on upstream concentration and substitutability (Carvalho et al., 2021).
To make the mechanics concrete, the following code constructs a stylized scale-free supply network, computes degrees and betweenness centrality to flag potentially critical suppliers, and visualizes the topology. The objective is pedagogical: the structure is synthetic, but the diagnostics map to real-world exercises where firms map their first- to nth-tier suppliers and identify chokepoints.
suppressPackageStartupMessages({
library(igraph)
library(ggraph)
library(tidyverse)
library(scales)
})
set.seed(42)
n <- 300
g <- sample_pa(n, power = 1.15, m = 2, directed = FALSE)
E(g)$weight <- runif(ecount(g), 0.2, 1.0)
bet <- betweenness(g, normalized = TRUE)
deg <- degree(g)
V(g)$critical <- bet > quantile(bet, 0.95)
V(g)$size <- rescale(deg, to = c(2, 8))
ggraph(g, layout = "fr") +
geom_edge_link(alpha = 0.15) +
geom_node_point(aes(size = size, color = critical)) +
guides(size = "none", color = "none") +
theme_void()
The next experiment contrasts random failures with targeted disruptions that remove the highest-betweenness nodes, a stylized proxy for sanctions or chokepoint closures. The outcome variable is the relative size of the largest connected component, a coarse measure of connectivity and hence feasibility of flow.
giant_share <- function(graph) max(components(graph)$csize) / vcount(graph)
k_seq <- seq(0, 50, by = 5)
order_bet <- order(bet, decreasing = TRUE)
random_path <- sapply(k_seq, function(k) {
g2 <- delete_vertices(g, sample(V(g), k))
giant_share(g2)
})
targeted_path <- sapply(k_seq, function(k) {
g2 <- delete_vertices(g, order_bet[1:k])
giant_share(g2)
})
library(tidyr)
df_paths <- tibble(k = k_seq,
random = random_path,
targeted = targeted_path) |>
pivot_longer(-k, names_to = "scenario", values_to = "giant")
ggplot(df_paths, aes(k, giant, linetype = scenario)) +
geom_line(linewidth = 0.8) +
labs(x = "Nodes removed", y = "Largest component (share of nodes)") +
theme_minimal()The divergence of the two curves highlights why geopolitics matters. Random failures degrade connectivity gradually, but targeted removal of central hubs induces discrete fragmentation. In real settings, the latter corresponds to the closure of key ports, sanctions on dominant suppliers, or restrictions on strategic inputs. The implication is that mitigating tail risk demands either structural redundancy around such hubs or credible contingency pathways.
A complementary diagnostic quantifies reroute flexibility, defined as the availability of edge-disjoint paths between random source–destination pairs. The code below computes the average count of edge-disjoint paths, an interpretable measure of innate rerouting capacity in the current topology.
pairs <- replicate(200, sample(V(g), 2), simplify = FALSE)
k_disjoint <- sapply(pairs, function(p) {
suppressWarnings(edge_disjoint_paths(g, p[1], p[2]))
})
data.frame(mean_edge_disjoint_paths = mean(k_disjoint))A higher value signals that alternative non-overlapping paths exist when a primary corridor is disrupted, which is particularly relevant under export controls or chokepoint failures.
14.3 Measuring concentration and dependency
Concentration on a single country or supplier increases expected disruption loss. A standard measure is the Herfindahl–Hirschman Index (HHI) computed over import shares by partner. The code below illustrates the calculation and a simple counterfactual where a “China+1” reallocation reduces concentration.
toy_shares <- tibble(partner = c("China", "Vietnam", "Mexico", "EU"),
share = c(0.55, 0.15, 0.20, 0.10))
hhi0 <- sum(toy_shares$share^2)
china_plus1 <- toy_shares
china_plus1$share[china_plus1$partner == "China"] <- 0.40
china_plus1$share[china_plus1$partner == "Vietnam"] <- 0.25
hhi1 <- sum(china_plus1$share^2)
tibble(configuration = c("Baseline", "China+1"),
HHI = c(hhi0, hhi1))
# # A tibble: 2 × 2
# configuration HHI
# <chr> <dbl>
# 1 Baseline 0.375
# 2 China+1 0.272From a risk perspective, the relevant object is not the HHI per se but the induced change in the distribution of shortfall under plausible shock scenarios. A simple two-supplier illustration clarifies the logic. Suppose supplier A has share \(s_A\) and failure probability \(p_A\), supplier B has share \(s_B\) and failure probability \(p_B\). Under independence and a single-period horizon, the probability of a full stockout is \(p_A p_B\). Diversification decreases this quantity even if \(p_B\) exceeds \(p_A\), provided \(p_A p_B < p_A\). The code below uses a Monte Carlo experiment to make this transparent and to accommodate partial failures.
set.seed(7)
simulate_shortfall <- function(sA=0.7, sB=0.3, pA=0.15, pB=0.20, N=1e5) {
failA <- rbinom(N, 1, pA)
failB <- rbinom(N, 1, pB)
supply <- (1 - failA) * sA + (1 - failB) * sB
mean(supply < 0.5) # probability of shortfall below 50% of planned volume
}
baseline <- simulate_shortfall(sA=0.85, sB=0.15, pA=0.12, pB=0.20)
diversified <- simulate_shortfall(sA=0.60, sB=0.40, pA=0.12, pB=0.20)
tibble(configuration = c("Concentrated", "Diversified"),
prob_shortfall_below_50pct = c(baseline, diversified))
# # A tibble: 2 × 2
# configuration prob_shortfall_below_50pct
# <chr> <dbl>
# 1 Concentrated 0.121
# 2 Diversified 0.119In practice, failure probabilities are state-dependent and correlated, especially under geopolitical shocks. Nevertheless, the exercise clarifies that, absent perfect correlation, multi-sourcing reduces the probability mass in severe shortfall tails. The residual question is cost: diversification usually raises unit cost or coordination overhead, bringing us to the efficiency–resilience trade-off.
14.4 The efficiency–resilience trade-off
The canonical trade-off pits lean, low-cost architectures against buffered, flexible designs. Inventory policies, dual or multi-sourcing, capacity reservation, and regionalized production all impose opportunity costs that are visible in ordinary times and benefits that are realized in rare but impactful states of the world. The operations literature documents robust strategies that hedge both supply-side and demand-side risks via buffer stocks, flexible contracts, and prioritized capacity, complementing structural diversification (Tang, 2006). The viable supply chain formulation combines responsiveness, resilience, and sustainability to emphasize that post-shock recovery capabilities are as critical as pre-shock robustness (Ivanov, 2020). Conceptually, firms choose points along a resilience–efficiency frontier, but network interactions and policy shocks can shift the entire frontier.
A simple pedagogical simulation illustrates how a small investment in structural flexibility can reduce cascade risk. Consider a toy network and add a small number of backup links that are dormant in steady state but activated under disruption. The code below compares connectivity degradation with and without such latent backups, holding everything else constant.
set.seed(99)
g0 <- sample_pa(250, power = 1.1, m = 2, directed = FALSE)
bet0 <- betweenness(g0)
order_bet0 <- order(bet0, decreasing = TRUE)
# Add 1% latent backup links among randomly chosen node pairs (low probability in normal ops)
add_backups <- function(graph, frac=0.01) {
n <- vcount(graph); target <- round(frac * choose(n, 2))
added <- 0
while (added < target) {
pair <- sample(V(graph), 2)
if (!are.connected(graph, pair[1], pair[2])) {
graph <- add_edges(graph, c(pair[1], pair[2]))
added <- added + 1
}
}
graph
}
g_flex <- add_backups(g0, frac = 0.005)
giant_share <- function(graph) max(components(graph)$csize) / vcount(graph)
k_seq <- seq(0, 40, by = 4)
simulate_path <- function(graph, order_bet) {
sapply(k_seq, function(k) {
delete_vertices(graph, order_bet[1:k]) |>
giant_share()
})
}
path0 <- simulate_path(g0, order_bet0)
path_flex <- simulate_path(g_flex, order_bet0)
df <- tibble(k = k_seq,
baseline = path0,
flexible = path_flex) |>
pivot_longer(-k, names_to = "design", values_to = "giant")
ggplot(df, aes(k, giant, color = design)) +
geom_line(linewidth = 0.9) +
labs(x = "Targeted removals (betweenness order)",
y = "Largest component share") +
theme_minimal()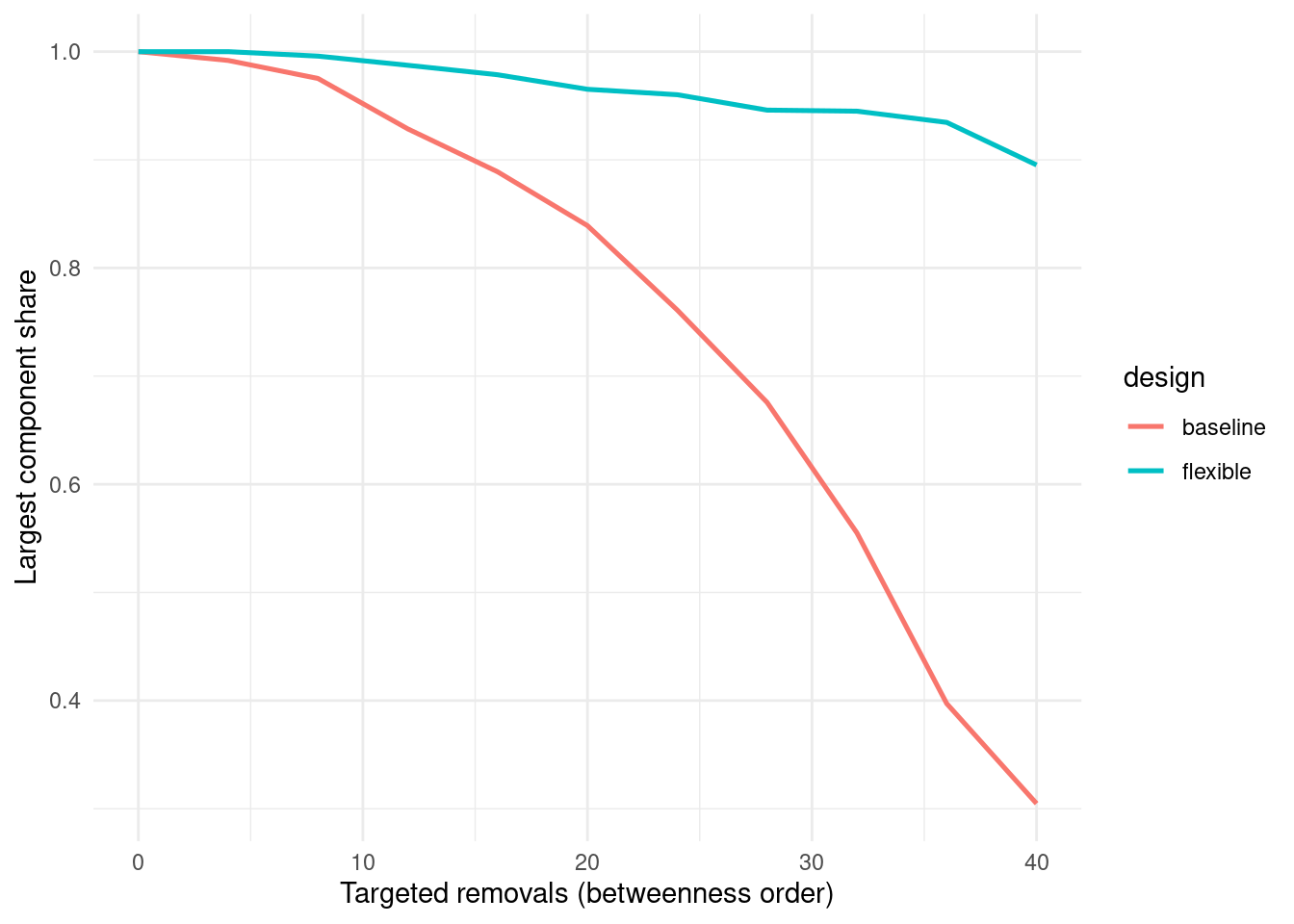
The flexible design, with a modest number of latent edges, exhibits slower fragmentation under targeted attacks. The lesson extends to real supply chains: duplicating a small subset of critical capabilities, or contracting for contingent capacity, shifts the resilience–efficiency frontier favorably even when such resources are underutilized in steady state.
14.5 Regionalization, friend-shoring, and modular architectures
Empirically, firms increasingly align supply nodes with major geopolitical regions, maintaining semi-autonomous “poles” with tighter intra-regional integration and looser inter-regional coupling. The macro-level intuition is modularity: regional clusters can localize shocks and facilitate governance and logistics within legal-institutional zones while diversifying exposure across blocs. This design accepts some loss of global economies of scale in exchange for credible containment of geopolitical risk. At the margin, friend-shoring—sourcing within aligned or low-tension jurisdictions—lowers the probability of policy-induced disruptions, albeit with sectorally varying feasibility. Institutional preconditions matter: trade agreements, standards mutual recognition, dispute settlement, and customs facilitation are the enabling technologies of regional modularity.
From a measurement perspective, one can track the regionalization of flows by monitoring the share of intermediate imports sourced within a bloc and the evolution of shipment lead-time dispersion. The code below sketches a template for retrieving a time series of goods exports and imports for a triad of economies, which can be adapted to regional aggregates or sectoral panels. The focus is on patterning rather than the precise econometric design; for empirical work, researchers will generally prefer bilateral trade with HS-level detail.
suppressPackageStartupMessages({
library(WDI)
library(dplyr)
library(ggplot2)
library(ggthemes)
})
countries <- c("US", "CN", "DE")
indicators <- c(exports = "NE.EXP.GNFS.KD", imports = "NE.IMP.GNFS.KD")
df_trade <- WDI(country = countries, indicator = indicators, start = 1995, end = as.numeric(format(Sys.Date(), "%Y")))
df_trade <- df_trade |>
rename(exports = NE.EXP.GNFS.KD, imports = NE.IMP.GNFS.KD) |>
mutate(country = factor(country, levels = countries))
ggplot(df_trade, aes(year, exports, group = country)) +
geom_line() +
facet_wrap(~country, scales = "free_y") +
theme_hc() +
labs(x = "Year", y = "Exports of goods and services (constant 2010 US$)",
title = "External orientation of selected economies")For concentration diagnostics by partner at the sector level, one would typically query a customs database and compute the HHI by partner for a set of HS codes associated with critical inputs. The pipeline below uses a generic pattern that you can adapt to a specific interface; in production work, you would replace the placeholder with an API call or a local file read.
# Pseudocode template for partner-level concentration diagnostics at HS level
# df <- read_csv("comtrade_hs8542_country_partner_year.csv") # HS 8542: integrated circuits
# df <- df |>
# group_by(year, reporter, partner) |>
# summarize(value = sum(trade_value_usd, na.rm = TRUE), .groups = "drop") |>
# group_by(year, reporter) |>
# mutate(share = value / sum(value, na.rm = TRUE)) |>
# summarize(HHI = sum(share^2), .groups = "drop")
# ggplot(df, aes(year, HHI, color = reporter)) + geom_line() + theme_minimal()This analysis quantifies whether partner diversification is increasing and can be overlaid with event windows around policy shifts to detect structural breaks.
14.6 Collaboration, visibility, and digital enablement
Relational contracts, information sharing, and joint risk management shift the effective frontier by reducing coordination frictions and enabling faster, better-targeted responses. The literature emphasizes that collaboration with multi-tier suppliers and logistics partners increases early-warning capacity and prioritization during crises, and that visibility platforms, control towers, and digital twins reduce information lags and mismatch across nodes (Pettit, Fiksel, & Croxton, 2010). Digitization is not a panacea under physical constraints, but in normal times it improves sensing, and in crises it enables reconfiguration that is otherwise infeasible.
To illustrate how visibility interacts with agility, the following code simulates a simple decision rule for rerouting under a port closure that increases travel time along a subset of edges. In the presence of real-time edge cost updates—an abstraction of digital visibility—the routing chooses alternate paths when their expected cost falls below the impaired primary. The gain is model-dependent, but the motif captures an important mechanism.
set.seed(11)
g2 <- sample_smallworld(1, 120, nei = 3, p = 0.05, loops = FALSE, multiple = FALSE)
E(g2)$time <- rexp(ecount(g2), rate = 1/5) # baseline travel time
# Impair a corridor: multiply times on a random cut set
impair_edges <- sample(E(g2), size = round(0.08 * ecount(g2)))
E(g2)$time_imp <- E(g2)$time
E(g2)$time_imp[impair_edges] <- E(g2)$time_imp[impair_edges] * 4
# Compare expected shortest-path times under baseline vs impaired network for random O-D pairs
pairs <- replicate(200, sample(V(g2), 2), simplify = FALSE)
sp_time <- function(graph, tattr) {
sapply(pairs, function(p) {
suppressWarnings(distances(graph, v = p[1], to = p[2], weights = E(graph)[[tattr]]))
})
}
baseline <- sp_time(g2, "time")
impaired <- sp_time(g2, "time_imp")
tibble(ratio = as.numeric(impaired / baseline)) |>
ggplot(aes(ratio)) + geom_histogram(bins = 30) +
labs(x = "Impaired / baseline shortest-path time",
y = "Count",
title = "Distribution of routing penalties under corridor impairment") +
theme_minimal()The histogram summarizes the penalty distribution. In a live setting, a control tower would trigger mode switches, supplier substitution, or inventory draws when the expected penalty exceeds a threshold, a rule that can be calibrated with service-level and cost targets.
14.7 Policy and institutional design
At the system level, the interplay of multilateral rules, regional agreements, and national industrial policy shapes firms’ feasible resilience sets. Institutions that reduce border frictions and harmonize standards expand the option set for multi-sourcing and within-bloc modularity. Conversely, sanctions, export controls, and meta-standard conflicts restrict feasible sets in ways that induce abrupt redesigns. Formal models and empirical evidence indicate that the welfare-optimal degree of diversification and localization is context-dependent; yet in most environments where tail risks are socially costly and private incentives underweight spillovers, calibrated incentives for diversification and contingency are warranted. The normative upshot is parsimonious: policies that preserve contestability and redundancy in critical nodes, mandate or subsidize modest buffers in life-critical supply chains, and maintain credible, transparent rules for crisis coordination are more likely to improve resilience without unduly sacrificing efficiency.
14.8 Putting it together: a minimal empirical workflow
Analytically, an integrated resilience program for an organization aligns four empirical streams. First, network mapping identifies tiered dependencies and critical nodes; the igraph-based routines above provide the minimal diagnostics. Second, concentration and dependency metrics quantify exposure at country–partner and supplier levels; the HHI sketch offers a baseline. Third, scenario libraries and drills translate geopolitically plausible events into operational shock parameters; the resilience index and routing penalty analyses provide templates for evaluation. Finally, monitoring pipelines track reconfiguration over time across volumes, lead times, and service levels; the trade series illustration indicates one track, while internal enterprise data furnish higher-frequency measures.
The synthesis is a portfolio problem. Firms select combinations of structural measures (multi-sourcing, regionalization, backups), buffer measures (strategic stocks, capacity options), and behavioral measures (collaboration, visibility, agility) that jointly optimize resilience subject to cost and feasibility. The evidence from network macroeconomics and operations suggests that small, well-placed structural redundancies, complemented by improved visibility and pre-negotiated contingencies, disproportionally reduce the tail risk associated with targeted geopolitical shocks (Acemoglu et al., 2012; Carvalho et al., 2021; Ivanov, 2020; Pettit et al., 2010; Tang, 2006).
14.9 Conclusion
The contemporary policy environment renders the old equilibrium of hyper-lean, globally stretched supply chains less robust than previously believed. The academic literatures on networks, institutions, and operations converge on a pragmatic prescription. First, treat resilience as a network property and diagnose structure; the presence of central chokepoints, low modularity, and limited reroute flexibility should trigger targeted redesign. Second, recognize that rules, credible commitments, and dispute-resolution mechanisms are not background conditions but inputs into the resilience production function; institutional quality expands the feasible set for diversification and coordination. Third, adopt portfolios rather than silver bullets; the combination of modest structural redundancy, calibrated buffers, visibility, collaboration, and agility shifts the resilience–efficiency frontier. The code provided demonstrates in stylized form how to implement diagnostics and to quantify counterfactuals that make these trade-offs transparent. The appropriate degree of redundancy and regionalization is sector- and firm-specific, but the central qualitative insight is general: in a geopolitical age, supply chain design must internalize the possibility of targeted, policy-induced shocks that exploit network structure. The organizational and policy task is to engineer architectures and rules that make such shocks less damaging and recovery more rapid, with due regard for cost and competitiveness.
Appendix: Reproducibility notes and additional code
The following global chunk settings make plots reproducible and suppress non-essential output.
A minimal function to compute an area-based resilience index for any observed performance time series is included for convenience.
A sketch for computing supplier-level concentration within firm procurement data is provided; this assumes a transactional dataset with supplier identifiers and spend.
# df_txn <- read_csv("firm_procurement_transactions.csv") # columns: date, supplier_id, spend_usd, category
# library(dplyr)
# df_supp <- df_txn |>
# group_by(supplier_id) |>
# summarize(spend = sum(spend_usd, na.rm = TRUE), .groups = "drop") |>
# mutate(share = spend / sum(spend))
# firm_hhi <- sum(df_supp$share^2)
# firm_hhiFinally, a toy routine to probe how the size of a pre-positioned buffer interacts with recovery time, given a simple demand and supply shock process, is included to help calibrate inventory policies.
set.seed(777)
simulate_buffer <- function(buffer_days = 10, horizon = 120, mu_d = 1000, sigma_d = 150,
cap = 900, shock_start = 1, shock_end = 40, cap_shock = 500) {
demand <- pmax(rnorm(horizon, mu_d, sigma_d), 0)
capacity <- rep(cap, horizon)
capacity[shock_start:shock_end] <- cap_shock
stock <- numeric(horizon); stock[1] <- buffer_days * mu_d
fill <- numeric(horizon)
for (t in 1:horizon) {
available <- capacity[t] + ifelse(t == 1, stock[1], stock[t-1])
fill[t] <- min(demand[t], available)
stock[t] <- max(available - demand[t], 0)
}
data.frame(t = 1:horizon, demand, fill, stock)
}
df_buf <- simulate_buffer(buffer_days = 12)
df_buf |>
pivot_longer(c(demand, fill), names_to = "series", values_to = "value") |>
ggplot(aes(t, value, linetype = series)) +
geom_line() +
labs(x = "Day", y = "Units", title = "Service performance with a 12-day buffer under a 40-day supply shock") +
theme_minimal()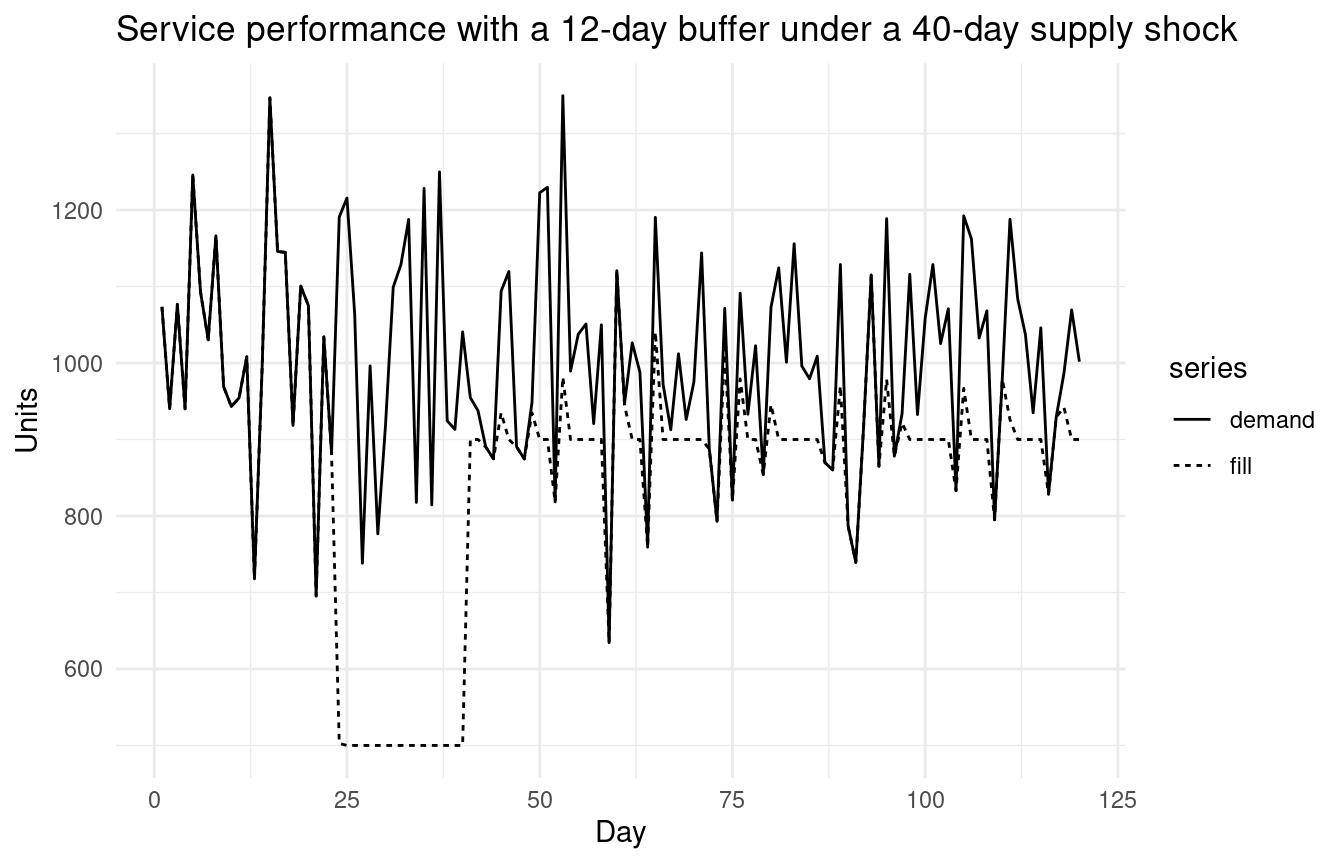
References
Acemoglu, D., Carvalho, V. M., Ozdaglar, A., & Tahbaz-Salehi, A. (2012). The network origins of aggregate fluctuations. Econometrica, 80(5), 1977–2016.
Antràs, P., & Chor, D. (2013). Organizing the global value chain. Econometrica, 81(6), 2127–2204.
Carvalho, V. M., Nirei, M., Saito, Y. U., & Tahbaz-Salehi, A. (2021). Supply chain disruptions: Evidence from the Great East Japan Earthquake. Quarterly Journal of Economics, 136(2), 1255–1321.
Farrell, H., & Newman, A. L. (2019). Weaponized interdependence: How global economic networks shape state coercion. International Security, 44(1), 42–79.
Ivanov, D. (2020). Viable supply chain model: Integrating resilience and sustainability perspectives—Lessons from COVID-19. International Journal of Production Research, 58(10), 2905–2915.
Pettit, T. J., Fiksel, J., & Croxton, K. L. (2010). Ensuring supply chain resilience: Development of a conceptual framework. Journal of Business Logistics, 31(1), 1–21.
Tang, C. S. (2006). Perspectives in supply chain risk management. International Journal of Production Economics, 103(2), 451–488*.