Chapitre 8 Innovation, normes et verrouillage technologique

À retenir

Toute société a besoin d’innovation pour croître. Les gouvernements convaincus ont décidé d’accompagner et de soutenir l’innovation par des politiques industrielles et de propriété intellectuelle. Toutefois, comme toujours en économie, ce qui semble évident au premier abord donne en fait des résultats différents en raison de la dynamique des acteurs du marché. L’innovation, qu’elle soit radicale ou incrémentale, est un outil stratégique aussi important que les autres stratégies de l’entreprise.

8.1 Introduction

L’innovation est très souvent associée à la notion d’entrepreneur (Redlich 1951), quoiqu’elle soit en fait bien plus vaste. Le premier à avoir défini l’innovation dans son sens économique et comme intégrant le processus de marché est assurément Schumpeter (1939). Il considérait que l’innovation était caractérisée par :

• la construction de nouvelles usines et de nouveaux équipements;
• l’introduction de nouvelles entreprises;
• l’apparition de nouveaux meneurs dans les entreprises.

Il voyait l’innovation comme étant différente de l’invention (Robertson 1967).

Quelle est la différence entre l’innovation et l’invention? Selon Roland (1977), invention et innovation ne devraient pas être séparées, même que l’innovation a une dimension plus large que l’invention. Une invention est une innovation, mais une innovation peut aussi être non technologique. Les innovations concernent aussi bien les produits que les processus de production.

Comment mesure-t-on l’innovation? Trois grandes voies se dégagent dans la littérature empirique. La première est de mesurer les dépenses en recherche et développement (RD). La deuxième est de mesurer le nombre de brevets déposés au cours d’une période donnée. La troisième est plus globale et consiste à interroger directement les entreprises par questionnaire afin d’analyser les innovations sur les produits et sur les processus de production (Mairesse and Mohnen 2002).

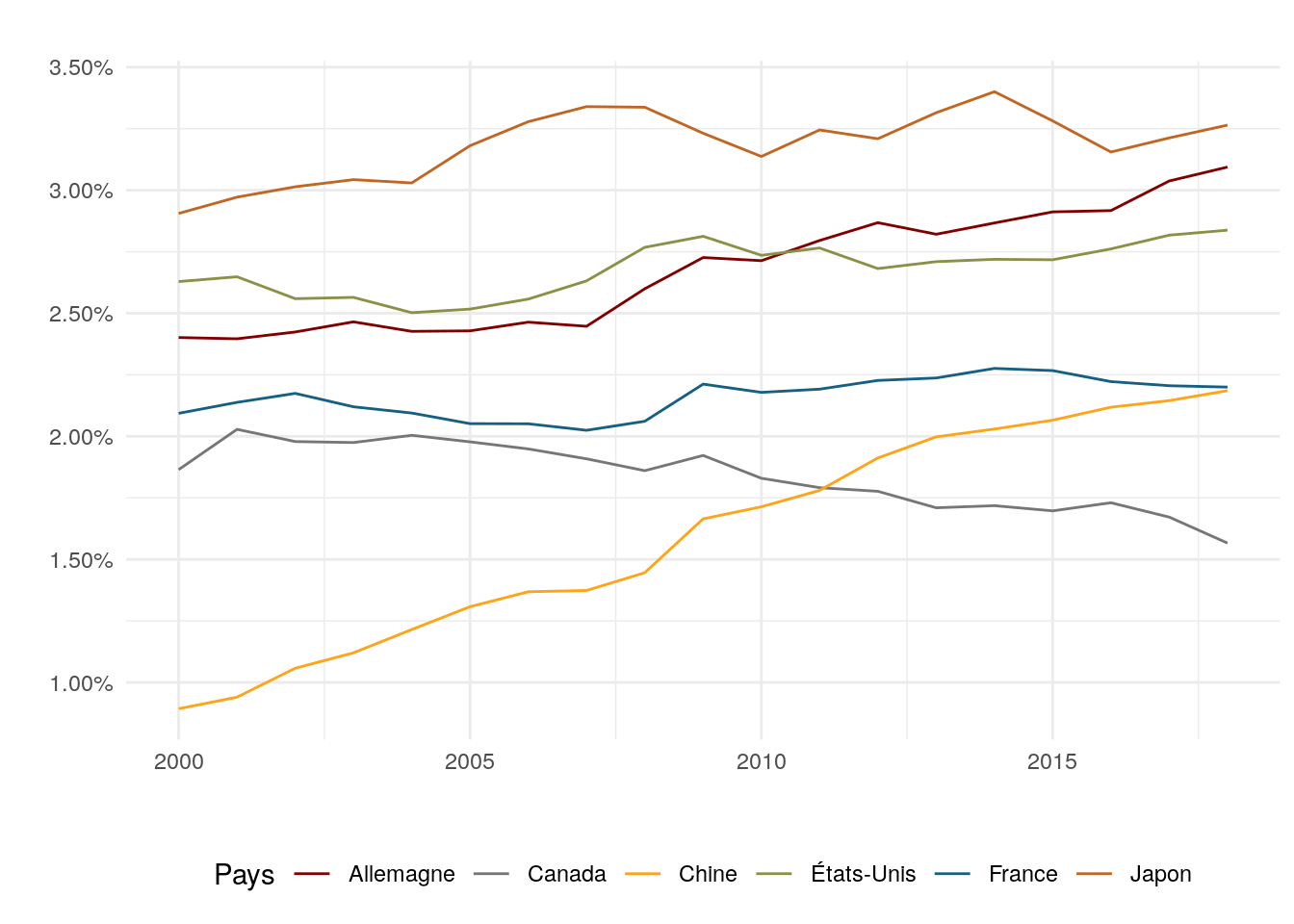
Figure 8.1: Dépenses en R&D par pays en % du PIB

Source : Warin, Thierry (2020): WDI R Package: A Use Case. figshare. Dataset. https://doi.org/10.6084/m9.figshare.12885299.v1

[code]

# Chargement des packages
library(WDI)
library(ggplot2)
library(ggsci)
library(gsheet)
library(dplyr)

# Chargement des données
df <- WDI(indicator = "GB.XPD.RSDV.GD.ZS", country = c("FR", "CA", "US","CN", "JP", "DE"), start = 2000, end = 2020)

# Renommer la colonne
colnames(df) <- c("ISO", "nameEng", "value", "year")

# Arrangement des données
df$year <- lubridate::ymd(df$year, truncated = 2L)
df <- na.omit(df)
df$value <- df$value / 100

# Chargement des noms de pays en français
ref <- gsheet2tbl("https://docs.google.com/spreadsheets/d/1sPNet_GHXm14YEAWqM0zSTR9c4bpa0z4CaJ_ajeWKq8/edit#gid=0")
ref <- select(ref, ISO, nameFra)
df <- left_join(df, ref, by = "ISO")

# Renommer la colonne
names(df)[5] <- "country"

# Création du graphique
ggplot(data=df, aes(x=year, y=value, color = country)) +
  geom_line()+
  xlab("") + 
  ylab("") +
  ggtitle("") +
  theme_minimal() + 
  theme(legend.position="bottom") +
  scale_color_uchicago() + 
  scale_y_continuous(labels = scales::percent) + 
  guides(col = guide_legend("Pays", nrow = 1))

8.2 Innovation

La typologie suivante permettra de mieux comprendre l’importance de l’innovation dans la dynamique des marchés et les avantages du processus concurrentiel.

Innovation radicale et innovation incrémentale. L’innovation peut se décliner en deux catégories. Il y a d’abord les innovations dites « radicales » ; par exemple, le lancement d’un réseau mondial de satellites pour offrir un service de téléphonie mobile (projet Iridium) marque un tournant pour la concurrence dans la radiotéléphonie, comme la télévision a pu révolutionner la communication. Ces innovations, brutales pour les structures de marché existantes, sont également appelées «innovations de rupture » (fig. 8.2). La courbe de coût marginal est beaucoup plus basse après l’introduction de l’innovation radicale qu’avant.

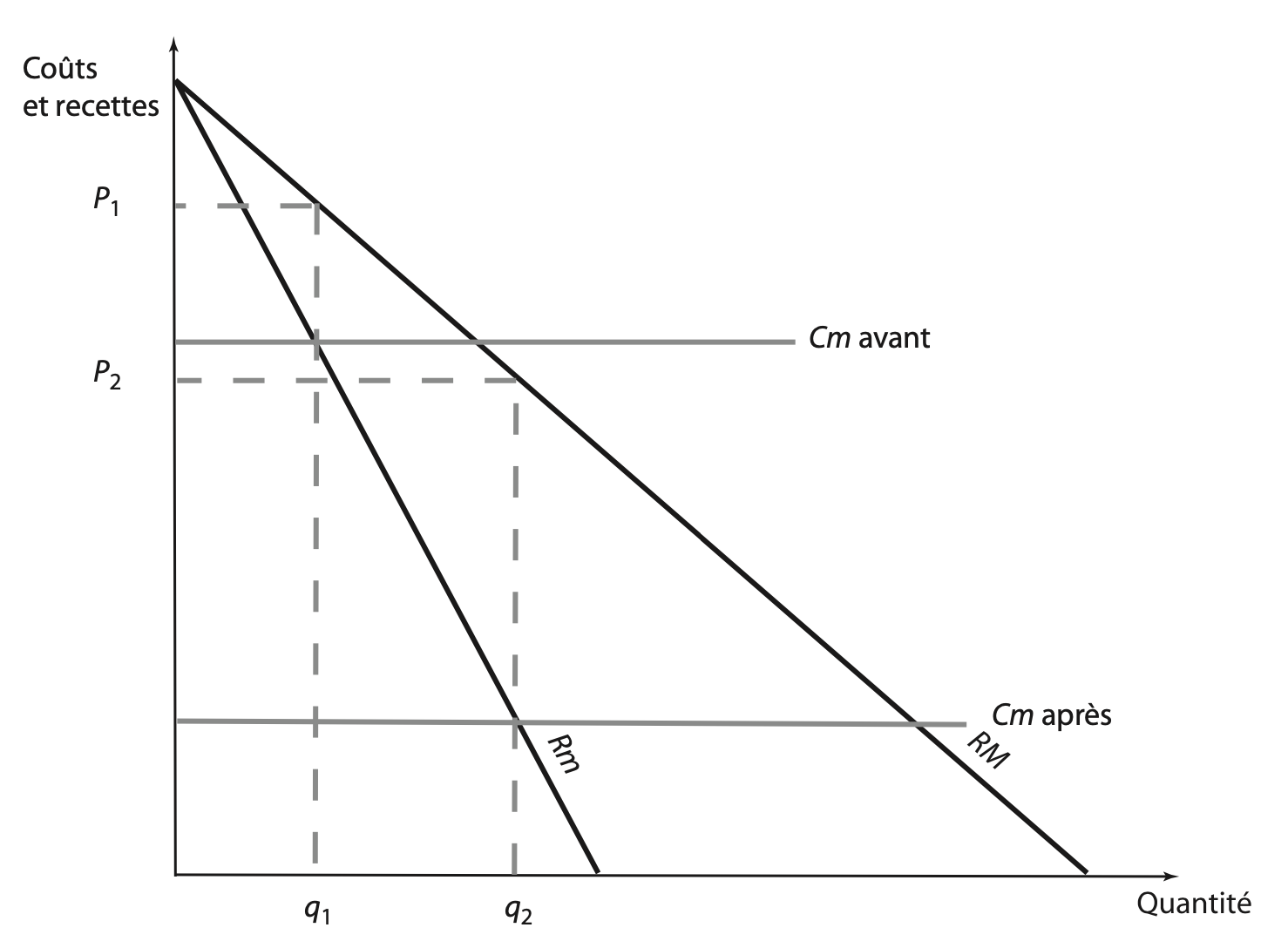
Figure 8.2: Introduction d’une innovation radicale.

Ensuite, il existe des innovations dites «incrémentales». On peut citer l’exemple d’un opérateur qui améliore jour après jour la productivité de son poste de travail à force de pratique⁵⁷. La courbe de coût marginal va être un peu plus basse après l’intro- duction de l’innovation qu’avant, l’objectif étant de la faire descendre le plus possible (fig. 8.3). Toutefois, si l’on compare avec l’introduction d’une innovation radicale, la courbe de coût marginal descend moins, au moins au début du processus.

Il faut plutôt chercher la véritable source de la compétitivité que recèle l’innovation dans ces petites améliorations générées au quotidien, dans l’interaction avec les autres acteurs de l’entreprise ou dans le dialogue technique avec le fournisseur. Les Japonais ne s’y sont pas trompés. Sous le terme de kaizen, ils désignent précisément les «petites innovations en continu» comme le moteur principal de la compétitivité. Des boîtes à idées aux prix annuels de l’innovation, du soutien à l’intraprenariat (Burgelman and Sayles 1986) à la gestion de projet, les initiatives managériales abondent pour tenter de relever le défi de l’innovation.

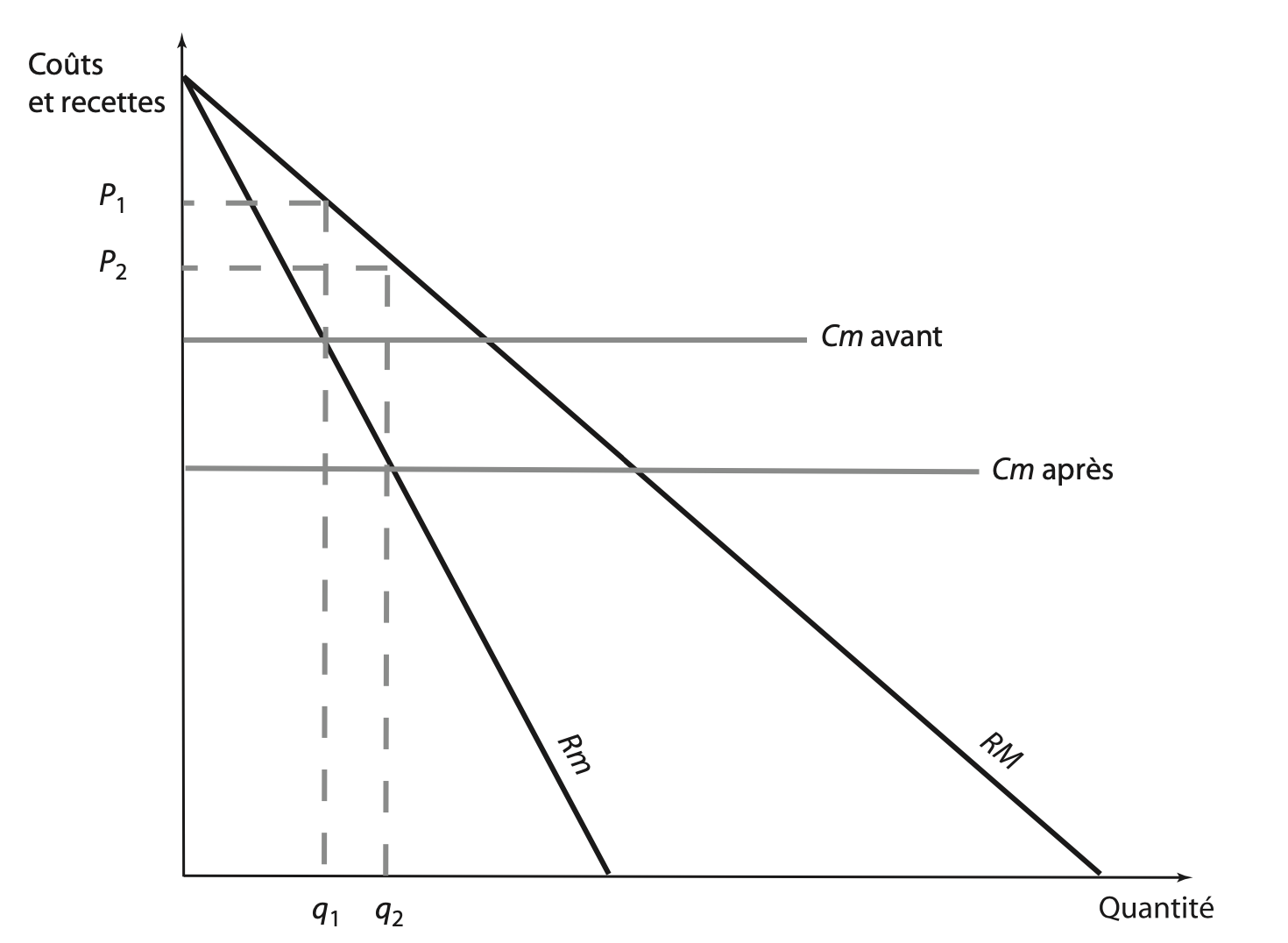
Figure 8.3: Introduction d’une innovation incrémentale.

Innovation technologique et innovation organisationnelle. L’innovation est souvent associée à la technologie. En parallèle à l’innovation en continu, les gains de compétitivité les plus conséquents obtenus dans nombre de secteurs et d’entreprises relèvent d’innovations purement technologiques. L’innovation porte, en effet, fréquemment sur le concept de produit proposé au client, par exemple «Internet» ou « Intranet », ou sur le procédé de fabrication, comme le recours au silicium pour les circuits imprimés des microprocesseurs. Pour autant, les innovations technologiques ne s’opposent pas aux innovations en continu qui en sont, d’ailleurs, souvent à l’origine. L’industrie des microprocesseurs n’est pas passée du «8088» à 4,77 MHz au «Pentium Dual-Core» à 4 GHz du jour au lendemain. C’est le processus d’apprentissage qui a rendu possible cette évolution. Les ingénieurs maîtrisant de mieux en mieux la technologie ont pu, à coup de petites innovations, de rationalisations de la production, offrir des cadences plus élevées.

L’innovation peut aussi porter sur l’organisation. Les flux tendus et le juste à temps, l’ingénierie simultanée, la qualité totale sont autant d’innovations organisationnelles qui se sont avéré constituer des voies de progrès particulièrement efficaces. Par exemple, Federal Express et, par la suite, ses concurrents ont introduit un nouveau service, celui du courrier rapide, sans pour autant mettre en oeuvre une technologie révolutionnaire, mais en se dotant d’une organisation logistique très pointue.

Du livre électronique à la tablette tactile flexible (Sources : plasticlogic.com, Libération 2013 Johnson 2012 et Kozlowski 2018)

Il aura fallu 6 années et 100 millions de dollars d’investissement pour que la firme britannique Plastic Logic arrive à mettre au point une tablette tactile flexible. En partenariat avec le fabricant de semi-conducteurs Intel, Plastic Logic s’est basé sur les travaux de chercheurs de l’Université de Cambridge développant des livres électroniques.

En 2008, son centre de production situé à Dresde, en Allemagne, a permis de mettre au point un matériau formé de fines couches de plastique dans lesquelles sont incorporées des matrices de semi-conducteurs. Ces derniers étaient activés pour représenter chaque pixel formant une image. Les feuilles de plastique pouvaient ainsi servir de tablettes électroniques flexibles afin de rendre la sensation de lecture virtuelle la plus fidèle possible : les pages du livre électronique tournaient lorsqu’un coin de la tablette est levé.

Ce médium léger, polyvalent et réutilisable à volonté (la feuille pouvant générer plus de 10 millions d’images au cours de son cycle de vie) permettait, selon la compagnie, d’ouvrir la voie à un remplacement progressif du papier dans l’industrie et à son adoption dans le milieu de la publicité comme solution de rechange aux écrans géants LCD.

Toutefois, ces tablettes tactiles flexibles n’ont pas réussi à percer le marché. Ce produit a échoué mais la compagnie a octroyé depuis des licences sur sa technologie.

Innovation « concurrentielle ». Même si l’on peut imaginer qu’il est intéressant d’être le plus petit nombre de concurrents possible sur un marché, il n’en reste pas moins qu’une entreprise bénéficie des innovations des autres entreprises. Les opérateurs de téléphonie mobile rivalisent en matière d’innovation commerciale, se copiant les uns les autres et essayant d’attirer le plus grand nombre de clients avec une innovation pendant la période de temps où ils en ont un monopole temporaire. De plus, le «processus concurrentiel», cher à l’école de Chicago, délivre des informations sur les opportunités de profit, les orientations à prendre, les stratégies à mettre en place. S’appuyant sur la «main invisible», la concurrence est le moteur d’un processus de découverte et d’innovation. Un prolongement utile de ce processus (Tushman and Anderson 1986) est celui qui identifie d’une part la destruction créatrice de Schumpeter (1939), par laquelle le nouveau doit détruire l’ancien pour émerger, et d’autre part, le renforcement de l’existant.

8.2.1 Innovation et structures de marché

On peut considérer les vues de trois auteurs ici : Schumpeter (1939), Arrow (1962), et Stiglitz (1981).

Approche schumpetérienne. L’approche schumpetérienne consiste à déterminer la structure de marché qui incite le plus à l’innovation. Les conclusions sont les suivantes:

• les dépenses en RD sont plus généralement conduites par de grandes entreprises;
• les dépenses en RD sont plus généralement conduites dans des industries où les entreprises ont naturellement des parts de marché importantes, c’est-à-dire des industries à structure oligopolistique.

Dès lors, de grandes entreprises dominantes tendent à être à l’origine de dépenses en RD importantes.

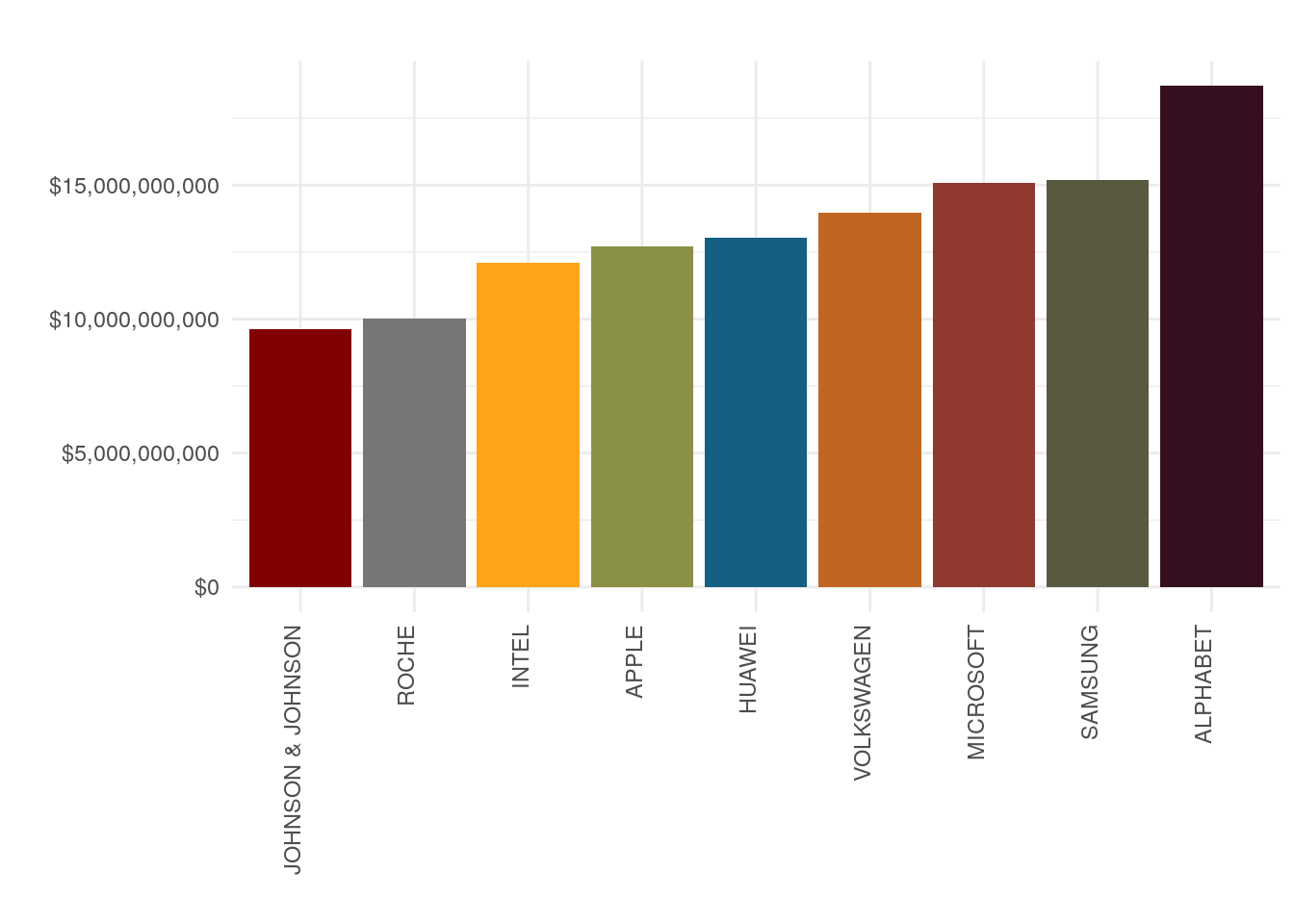
Figure 8.4: Dépenses en R&D par entreprise en USD en 2019

Source: Warin, Thierry (2020): iriR: An R Package for the EU Industrial Research and Industry Scoreboard. figshare. Dataset. https://doi.org/10.6084/m9.figshare.11774640.v4

[code]

# Chargement des packages
library(iriR)
library(dplyr)
library(ggplot2)
library(ggsci)

# Chargement des données
df <- iriR::irir_data(years = as.numeric(format(Sys.Date(), "%Y"))-1, indicators = "RD.usd")

# Renommer la colonne
names(df)[5] <- "company"
names(df)[3] <- "year"

# Garder le top 9 des companies
df <- filter(df, rank <= 9)

# Simplification du nom de l'entreprise
df$company <- gsub("HUAWEI INVESTEMENT & HOLDING CO", "HUAWEI", df$company)
df$company <- gsub("SAMSUNG ELECTRONICS", "SAMSUNG", df$company)

# Classer les données dans l'ordre croissant
df$company <- factor(df$company, levels = unique(df$company)[order(df$value)])

# Création du graphique
ggplot(data=df, aes(x=company, y=value, fill = company)) +
  geom_col()+
  xlab("") + 
  ylab("") +
  ggtitle("") +
  theme_minimal() + 
  theme(legend.position="none") +
  scale_fill_uchicago() + 
  guides(col = guide_legend(nrow = 1)) + 
  theme(axis.text.x = element_text(angle = 90, vjust = 0, hjust=1)) + 
  scale_y_continuous(labels = scales::dollar)

Analyse de Arrow. Dans l’analyse de Arrow, on se demande si l’hypothèse schumpetérienne est correcte, à savoir si l’innovation est affectée par la structure de marché.

Dans un marché concurrentiel, une entreprise n’innove que si le coût de l’innovation est inférieur à l’augmentation de profit provenant de l’innovation. Si les concurrents peuvent adopter l’innovation, il n’y aura pas d’augmentation de profit. En revanche, si l’innovation n’est pas transférable, alors l’entreprise aura un intérêt à investir afin de diminuer sa fonction de coût en raison de l’innovation et de tarifer à un prix inférieur à toutes les autres entreprises, se retrouvant en situation de monopole (quasi-concurrence monopolistique). Dans l’analyse de Arrow, une entreprise en situation de monopole accordera moins de valeur à une innovation qu’une entreprise en situation de concurrence, la première entreprise faisant déjà un profit de monopole.

Modèle de Stiglitz et Dasgupta. Dans le modèle de Stiglitz et Dasgupta, toutes les entreprises peuvent innover en même temps. Le profit des entreprises est représenté par:

\[\begin{equation} {\prod}_i = P(Q) \times q_i - C(x_i) \times q_i - X_i \tag{8.1} \end{equation}\]

où \(X_i\) est la dépense en RD de l’entreprise \(i\). Si toutes les entreprises dépensent le même montant \(X^*\) en RD, alors elles ont toutes le même coût \(C(X^*)\).

Si l’on résout la maximisation du profit comme dans un oligopole de Cournot à \(n\) entreprises, on obtient la quantité produite par chaque entreprise qui maximise son profit :

\[\begin{equation} q^* = \frac{a - C(x^*)}{b(n + 1)} \tag{8.2} \end{equation}\]

Pour déterminer la dépense optimale en RD, on prend la dérivée première de l’équation représentant le profit par rapport à \(X_i\) que l’on pose ensuite égale à 0 :

\[\begin{equation} \frac{\partial (P(Q) \times {q_i}^* - C(x_i) \times {q_i}^* - x_i)}{\partial x_i} = 0 \tag{8.3} \end{equation}\]

ce qui donne :

\[\begin{equation} - \frac{\partial C(x_i)}{\partial x_i} \times {q_i}^* = 1 \tag{8.4} \end{equation}\]

Le terme \(- \frac{\partial C(x_i)}{\partial x_i}\) est la diminution du coût marginal d’un dollar additionnel dépensé en RD. Par conséquent, le premier membre de l’équation précédente représente le bénéfice total d’un dollar supplémentaire dépensé en RD. À l’équilibre, ce bénéfice total doit être égal à 1.

Mais le plus important est que le bénéfice marginal \(- \frac{\partial C(x_i)}{\partial x_i} \times {q_i}^*\) dépend de \({q_i}^*\) et que ce dernier dépend du nombre d’entreprises dans l’industrie, \(\frac {a - C(x^*)}{b(n +1)}\).

Ainsi, plus il y a d’entreprises, plus \({q_i}^*\) est faible et donc plus les bénéfices de la RD seront faibles. Un bénéfice plus faible implique un investissement en RD inférieur. Stiglitz et Dasgupta (1981) viennent ainsi redonner toute vitalité à la thèse de Schumpeter.

8.2.2 Innovation et rendements d’échelle

Dans certains cas de figure, on a l’impression que les économies d’échelle sont infinies en raison de rendements d’échelle apparemment toujours croissants. Une entreprise qui vend sur Internet se retrouve face à un très grand public. En cas de coûts de développement fixes, elle voit son coût moyen baisser au fur et à mesure que ses ventes augmentent. Ce raisonnement s’applique plus facilement au secteur des services dont la production exclusivement immatérielle représente, la plupart du temps, un coût de développement fixe.

Pourtant, même sur ce type de marché, les rendements sont, certes, croissants au départ, mais finissent toujours par décroître. En revanche, ils mettent probablement plus de temps à le faire que pour une entreprise traditionnelle. Cela s’explique non pas du fait que cette propriété correspond à une typologie de marché spécifique (type économie des réseaux), mais que la cible (et donc les clients potentiels) est beaucoup plus large que dans l’économie traditionnelle et que les coûts pour atteindre cette cible sont inférieurs à ceux de l’économie traditionnelle (il s’agit de coûts de communication).

La clé réside donc bien dans la définition même des coûts de production. De nos jours, la fonction de production représente l’ensemble des processus permettant de transformer un intrant en un extrant directement livrable à un consommateur. Il est possible d’envisager que la fonction de production intègre les coûts de transaction de l’ensemble des étapes du processus de production, y compris les variables marketing, communication, etc. Ainsi, l’économie des réseaux a un champ d’analyse qui ne concerne pas les entreprises dont les rendements sont toujours croissants en raison du marché sur lequel elles se trouvent, mais qui touche les entreprises dont les rendements sont plus longtemps croissants que pour les autres entreprises. Au bout d’un certain temps, des coûts apparaissent, liés à la communication, à la fidélisation au service ou au produit, etc., diminuant les économies d’échelle.

La loi des rendements d’échelle décroissants garde tout son sens, même si les rendements d’échelle sont plus longtemps croissants sur Internet que dans l’économie traditionnelle en raison d’une cible plus large et de coûts de transaction réduits.

8.2.3 Innovation et stratégies de différenciation de produits

Si l’asymétrie d’information se réduit, il est intéressant de tenter de la recréer, car elle est une des sources de profit. On sait que la différenciation peut prendre deux formes : minimale ou maximale. Dans le premier cas, l’entreprise entrant sur le marché cherche à capter l’image de marque de ses concurrents. Elle se positionnera sur la même cible. Dans le second cas, l’entrant choisit un positionnement complètement différent de celui des entreprises en place. La mise en pratique de la différenciation se fait, entre autres, par la communication et les campagnes de marketing.

L’intensification de la concurrence sur les secteurs traditionnels mais aussi par les entreprises sur Internet donne un nouvel élan aux stratégies de différenciation. Les budgets alloués au positionnement et à la communication externe deviennent de plus en plus importants. L’objet principal d’une entreprise devient davantage la gestion d’une marque et de son positionnement par rapport à la concurrence qu’un outil de transformation d’un intrant en un extrant.

Faut-il faire de la différenciation maximale ou minimale ? Pour répondre à cette question, il est possible de reprendre les enseignements du modèle de Hotelling (1929). Quelles sont les hypothèses importantes? La première est celle qui concerne les coûts de transport et la seconde porte sur les prix. Passer d’un marché, l’économie traditionnelle, à un autre, Internet, est coûteux. Les «coûts de transport» sont donc positifs. De plus, les marchés n’étant pas les mêmes, les politiques de prix peuvent être différentes dans le but de capter toute la demande. La différenciation maximale entre l’offre sur un site Internet et celle qu’on trouve dans l’économie traditionnelle semble évidente. En effet, l’intérêt d’un site Internet est de bien faire comprendre au consommateur où se trouve l’accès au contenu ou au service.

Pour analyser, maintenant, le positionnement des sites d’un même secteur sur Internet, reprenons Hotelling (1929). La première hypothèse dans ce cas est qu’Internet représente des coûts de transport nuls pour le positionnement des entreprises le long de la ville linéaire. La seconde est qu’en raison des faibles coûts de transaction, les politiques de prix sont réduites. Il est donc possible de considérer que les prix sont fixes. Sous couvert de ces deux hypothèses, le modèle de Hotelling (1929) indique que la meilleure stratégie est celle de la différenciation minimale. Par conséquent, la différenciation doit être maximale entre des entreprises sur Internet et dans l’économie traditionnelle et minimale pour les entreprises d’un même secteur sur Internet.

8.3 Brevets et incitations à innover

Lorsqu’on parle de brevets, tout le monde est d’accord pour dire que cette protection de la propriété intellectuelle est essentielle à la promotion de l’innovation. Dans ce contexte, on entend souvent dire que la Chine, avec sa réputation de mauvais joueur en matière de respect de la propriété intellectuelle, serait la cause de tous les maux des pays occidentaux qui perdent leurs avantages comparatifs reliés à leur niveau d’innovation. La réalité est en fait un peu plus compliquée…

Il est indéniable que la protection accordée à un entrepreneur pour une innovation incite à l’innovation. En revanche, certains facteurs peuvent ralentir l’innovation. L’obtention de la protection requiert la divulgation du procédé de fabrication. Cette divulgation du procédé de fabrication et l’absence de protection dans certains pays peuvent réduire l’incitation à innover, en tout cas à innover dans des secteurs facilement imitables. De plus, une durée de protection trop longue peut aussi ralentir globalement l’innovation.

Enfin, il ne faut pas oublier qu’une grande partie de l’innovation d’un pays provient de la recherche fondamentale et n’est pas motivée par des considérations de rentabilité immédiate. Parfois même une entreprise va s’approprier cette recherche fondamentale en brevetant l’innovation et en bloquant toute nouvelle innovation pour la durée du brevet, si elle décide de ne pas investir d’argent en RD pour améliorer l’innovation.

Un retour vers l’innovation ? (Adapté de Jon 2012)

La domination de Microsoft des années 1980 jusqu’à l’apparition d’Android au milieu des années 2000 a attribué à la firme californienne une image de compagnie n’innovant que très peu et dont les produits comportaient plusieurs failles de sécurité.

Néanmoins, lorsque le quasi-monopole Wintel (alliance entre les processeurs Intel et le système d’exploitation Windows de Microsoft) était en chute libre en matière de parts de marché (50 % des ordinateurs personnels en 2011 face à Android et Apple), l’entreprise a du se positionner à nouveau sur l’échiquier de l’innovation.

Ce retour à l’innovation semblait être la solution pour faire face à la perte de parts de marché, tandis qu’un manque d’innovation pendant une trentaine d’années semblait avoir été dicté par sa domination écrasante dans l’industrie.

On retient les brevets comme un élément important de la politique industrielle d’un pays. Aux brevets s’ajoutent les droits sur la propriété intellectuelle (droits d’auteur) et la protection des marques de commerce.

L’aspirine

Un exemple flagrant, et extrême à la fois, de la difficulté à définir la propriété intellectuelle est celui de l’aspirine. Hippocrate (460 av. J.-C.) découvre les bienfaits d’une substance qu’il extrait des saules pleureurs. En 1828, Johann Buchner, professeur de pharmacie à l’Université de Munich, parle de salicine. Avant cela, deux chercheurs italiens, Brugnatelli et Fontana, avaient isolé la salicine dans une forme toutefois impure. En 1829, Henri Leroux améliore l’extraction de salicine, et en 1838, Rafaele Piria, travaillant à la Sorbonne, synthétise l’acide salicylique. Toutefois, l’acide est trop corrosif pour l’estomac, et un chimiste français, Charles Gerhardt, va améliorer en 1853 la formule pour obtenir l’acide acétylsalicylique. En 1889, un chimiste allemand, Felix Hoffmann, qui travaille pour Bayer, redécouvre la formule. En 1899, Bayer dépose un brevet et change le nom pour «Aspirine». Après la Première Guerre mondiale, le Traité de Versailles de 1919 forcera Bayer à abandonner son brevet et la protection de marque de commerce sur l’aspirine.

8.3.1 Réglementations

Un brevet est un titre de propriété industrielle qui confère à son titulaire un droit exclusif d’exploitation sur l’invention brevetée. Ce titre a une durée limitée, généralement 20 ans, voire 25 ans dans le cas de certains produits pharmaceutiques. Le brevet n’est valable que sur un territoire déterminé (en général un pays unique, parfois un groupe de pays, comme dans le cas du brevet eurasien).

Le premier brevet industriel fut délivré en 1421 à Florence, et c’est l’architecte et ingénieur Filippo Brunelleschi qui l’obtint pour une invention dans le domaine de la manutention de marchandises destinées au transport par bateau. Plus tard, c’est à Venise que fut octroyé un deuxième brevet, lorsqu’en 1469 la Ville accorda à un assistant de Gutenberg, pour la durée de sa vie, le privilège d’imprimer, à l’exclusion de tout autre, au moyen d’un système utilisant des caractères mobiles.

Les souverains européens accordaient des «lettres de brevets» aux inventeurs. Ces lettres avaient le sceau royal, et bien souvent duraient toute la vie de l’inventeur.

La première réglementation sur les brevets aux États-Unis est l’oeuvre de Thomas Jefferson : le U.S. Patent Act de 1790. Avant cela, le roi d’Angleterre était le propriétaire de toutes les inventions créées par les habitants des colonies. Le premier brevet américain a été attribué à Samuel Hopkins de Pittsford, dans le Vermont (Nouvelle-Angleterre), qui avait inventé un engrais. Le coût de dépôt du brevet était de quatre dollars de l’époque. Après le Patent Act du 4 juillet 1836, les brevets ont été numérotés. Le numéro 1 a été accordé le 13 juillet 1836 à John Ruggles pour un système de poulies.

En ce qui concerne les droits d’auteur, ils confèrent à un créateur les droits exclusifs sur la production, la publication ou la vente de ses travaux artistiques, littéraires, ou musicaux. En France, ils sont régis par la loi de 1957. Aux États-Unis, les droits d’auteur conférés aux entreprises durent 95 ans, et pour les individus ils le sont à vie plus 70 ans après la mort. Le cas du décès de Walt Disney, qui était à la tête de l’empire Disney, a nécessité un changement de la législation américaine afin d’éviter que tout un chacun puisse reproduire librement Mickey.

Pour ce qui est des logiciels, ils sont sous le coup des droits d’auteur aux États-Unis et en Europe. Ils peuvent être brevetés aux États-Unis, mais pas en Europe (article 53 de la Convention de Munich du 5 octobre 1973). La protection des droits d’auteur interdit à quiconque de reproduire le code, mais autorise la production d’un logiciel faisant à peu près la même chose. La protection du brevet interdit quant à elle la production d’un logiciel faisant la même chose ! On mesure ici l’enjeu de l’attribution de brevets aux producteurs de logiciels en plus des droits d’auteur.

Quant aux marques de commerce, les mots et les symboles qui permettent la distinction d’un bien ou d’un service sont protégés. La protection n’expire pas, mais une entreprise peut perdre la propriété « pratique » d’une marque si son produit devient la norme et tombe dans le langage commun : mobylette, frigidaire, walkman, etc. On peut se demander si «iPad» deviendra un jour le nom commun servant à désigner une tablette.

Brevet canadien⁵⁸. L’Office de la propriété intellectuelle (OPIC) est l’organisme gouvernemental délivrant les brevets au Canada. À compter de la date de dépôt de la demande de brevet, l’invention est protégée pour une période de 20 ans, aussi longtemps que les taxes de maintien sont payées annuellement. La protection du brevet n’est effective que sur le territoire canadien. Dix-huit mois après le dépôt de la demande de brevet, le brevet devient public afin de favoriser la diffusion des connaissances. Néanmoins, le titulaire du brevet reste la seule personne pouvant fabriquer et commercialiser les fruits du brevet au cours de cette période de protection.

Afin de breveter une invention canadienne à l’étranger, on peut déposer une demande au Bureau des brevets en vertu du Traité de coopération en matière de brevets administré par l’Organisation mondiale de la propriété intellectuelle. Cette procédure permet de breveter l’invention dans les 142 pays signataires du traité.

Brevet français. En France, la procédure de délivrance de brevets est effectuée par l’Institut national de la propriété intellectuelle (INPI). En France comme dans la plupart des pays, les déposants nationaux optent majoritairement pour la voie nationale. Ils représentent 80% des dépôts effectués à l’INPI. Le brevet français confère une protection de 20 ans sur le territoire national, à partir de la date de dépôt. Une fois la demande de dépôt effectuée, le déposant peut divulguer son invention sans craindre qu’un concurrent puisse l’exploiter librement. Les demandes de dépôt sont publiées 18 mois plus tard dans le Bulletin officiel de la propriété industrielle (BOPI).

Les entreprises françaises utilisent souvent la procédure nationale comme première étape, afin d’obtenir, avant l’expiration du délai de priorité, le rapport de recherche établi par l’Office européen des brevets (OEB) qui leur permet d’apprécier la pertinence d’une extension de leur brevet à l’étranger. Le déposant dispose d’une priorité de 12 mois pour étendre la protection en Europe ou à l’international, tout en gardant le bénéfice du premier déposant. C’est la date du dépôt qui enclenche la protection.

Dans le cadre de la procédure européenne, il est possible de désigner un grand nombre de pays (ou même tous les pays membres de l’OEB) au départ et de valider ultérieurement ces choix, en ne retenant finalement que les pays pour lesquels on désire réellement une protection. Cette validation intervient au moment de l’obtention du brevet européen, c’est-à-dire trois à cinq ans plus tard dans la pratique.

En contrepartie de l’obtention du droit exclusif d’exploitation, l’invention doit être divulguée au public : les brevets sont automatiquement publiés 18 mois après la date de priorité, c’est-à-dire le premier dépôt, sauf cas particuliers.

Le tableau 8.1 présente l’évolution des délivrances de brevets français⁵⁹. En moyenne, les délivrances interviennent entre 24 et 30 mois après le dépôt.

Table 8.1: Demandes et délivrances de brevets en France

	2014	2015	2016	2017	2018	Variation 2017-2018
Demandes de brevet
Résidents	25116	25085	24714	25040	24741	-1.2%
Non-résidents	2033	1994	2012	1832	1919	4.7%
À l’étranger	47193	47465	46795	46047	44379	-3.6%
Brevets délivrés
Résidents	15298	16468	17656	17530	19186	9.4%
Non-résidents	1319	1656	1751	1649	1675	1.6%
À l’étranger	26845	27491	29981	30046	31198	3.8%

Source: OMPI. Statistiques de propriété intellectuelle par pays - France.

[code]

# Chargement des packages
library(gsheet)
library(tidyverse)
library(kableExtra)

# Chargement des données
df <- gsheet2tbl("https://docs.google.com/spreadsheets/d/12b48gT4sTt-tDn8ufBq9hT-VTVEAbYQbwLLZnDt2iJU/edit#gid=963176122")

# Manipulation des données
dt <- filter(df, Année == max(df$Année) | Année == max(df$Année)-1 | Année == max(df$Année)-2 | Année == max(df$Année)-3 | Année == max(df$Année)-4)

dt <- dt %>%
  pivot_longer(-c(Type, Année), names_to = " ", values_to = "Nombre")

dt <- dt %>%
  pivot_wider(names_from = Année, values_from = Nombre)

# Cacul de la variation des deux dernières années
variation <- (dt[,ncol(dt)] - dt[,ncol(dt)-1]) / dt[,ncol(dt)-1] * 100
names(variation)[1] <- paste0("Variation ", max(df$Année)-1, "-", max(df$Année))
variation$`Variation 2017-2018` <- paste(round(variation$`Variation 2017-2018`, digits = 1), "%", sep="")

# Combiner les deux tableaux de données
dt <- cbind(dt, variation)

# Création du tableau
kable(dt[,2:ncol(dt)], align=rep('c', 6), caption = "Demandes et délivrances de brevets en France") %>%
  kable_styling("striped") %>%
  pack_rows("Demandes de brevet", 1, 3) %>%
  pack_rows("Brevets délivrés", 4, 6)

Brevet européen. La voie européenne est régie par la Convention sur le brevet européen du 5 octobre 1973 et gérée par l’OEB. Le dépôt européen permet d’obtenir un brevet européen pour tous les pays désignés parmi les 31 possibles (au 31 décembre 2005), à partir d’un seul dépôt (rédigé en français, en anglais ou en allemand) et par une seule procédure. Ce brevet européen sera ensuite éclaté en autant de brevets nationaux que de pays désignés⁶⁰. Les demandes européennes sont de deux types : demandes euro-PCT et demandes euro-directes. Une demande euro-PCT (Patent Cooperation Treaty) est une demande de brevet internationale selon la procédure gérée par l’Organisation mondiale de la propriété intellectuelle (OMPI) et contenant une désignation européenne en vue d’une protection d’un pays comme la France, par exemple. Une demande euro-directe est une demande qui entre directement à l’OEB sans passer par la voie PCT : ce peut être une demande déposée directement à l’OEB ou une demande sous priorité. Une proportion importante des demandes euro-PCT sont abandonnées à un stade précoce de la procédure internationale. On appelle « demandes européennes entrées en phase régionale» l’ensemble des demandes euro-PCT et euro-directes qui sont réellement entrées dans le processus de délivrance d’un brevet européen. La France est désignée dans la quasi-totalité de ces demandes. Le tableau 8.2 illustre la dynamique de la voie européenne.

Table 8.2: Évolution des demandes européennes de brevets

Source: European Patent Office. European patent applications 2010-2019 per country of residence of the applicant.

[code]

# Chargement des packages
library(gsheet)
library(dplyr)
library(reactable)

# Chargement des données
df <- gsheet2tbl("https://docs.google.com/spreadsheets/d/12b48gT4sTt-tDn8ufBq9hT-VTVEAbYQbwLLZnDt2iJU/edit#gid=1517739213")

# Chargement des noms de pays en français
ref <- gsheet2tbl("https://docs.google.com/spreadsheets/d/1sPNet_GHXm14YEAWqM0zSTR9c4bpa0z4CaJ_ajeWKq8/edit#gid=0")
ref <- select(ref, ISO, nameFra)

# Concaténation des deux tableaux de données
df <- left_join(df, ref, by = "ISO")

# Renommer la colonne nameFra par Pays
names(df)[ncol(df)] <- "Pays"

# Remplacer la valeur manquante par Namibie
df[["Pays"]][is.na(df[["Pays"]])] <- "Namibie"

# Sélection des dernières années
n_5 <- ncol(df)-1
n_1 <- ncol(df)-10
df <- subset(df, select=c(ncol(df), n_5:n_1))

# Création du tableau
sticky_style <- list(position = "sticky", left = 0, background = "#fff", zIndex = 1,
                     borderRight = "1px solid #eee")

reactable(df, 
          searchable = TRUE, 
          highlight = TRUE,
          striped = TRUE,
          showPageSizeOptions = TRUE, 
          pageSizeOptions = c(6, 10), 
          defaultPageSize = 6,
          defaultSortOrder = "desc", 
          defaultSorted = "2019", 
          columns = list(
            Pays = colDef(
              style = sticky_style,
              headerStyle = sticky_style)))

Brevet international. La procédure internationale (PCT), gérée par l’OMPI, est une procédure de dépôt d’une demande de brevet en une seule démarche auprès de pays choisis parmi plus d’une centaine susceptibles d’être désignés, sans devoir initialement remettre de traduction de la demande ni payer de taxes nationales (tabl. 8.3). La phase d’instruction internationale commune est suivie par une procédure auprès de chacun des pays désignés. Lorsqu’un pays de l’OEB est désigné (par exemple la France), le dépôt entre dans le système européen des brevets. Pour beaucoup de déposants, la procédure PCT est devenue le moyen privilégié de déposer à l’étranger, car il permet de retarder les procédures nationales. En effet, l’intérêt de la voie PCT réside dans la possibilité d’attendre jusqu’à 30 mois avant de rentrer dans les phases nationales où il faut confirmer les désignations par le paiement des taxes propres à chaque pays. Elle permet donc au déposant de confirmer ou non les désignations initiales sur la base d’une meilleure appréciation de la concurrence, des marchés et de la valeur économique de la demande de brevet. Depuis le 1er janvier 2004, ces désignations sont devenues automatiques. Dans la pratique, nombre de ces désignations ne seront pas confirmées : elles correspondent donc à des demandes que l’on pourrait qualifier de «virtuelles». Lorsqu’elle est confirmée, la demande désignant la France va entrer en phase régionale dans le système OEB : elle débouchera sur la délivrance d’un brevet européen. Les dépôts à l’OMPI ont connu une croissance très forte depuis la mise en place du système PCT en 1978. Il faut y voir d’abord l’effet du phénomène de mondialisation, qui fait que les déposants recherchent la protection du brevet dans un nombre croissant de pays. La croissance des dépôts a également été stimulée par un flux constant d’adhésions de nouveaux États membres et par les décisions successives de réduction des taxes de désignation.

Table 8.3: Évolution des dépôts de brevets par la voie internationale

Source: OMPI. Base de données statistiques - PCT.

[code]

# Chargement des packages
library(gsheet)
library(reactable)

# Chargemment des données
df <- gsheet2tbl("https://docs.google.com/spreadsheets/d/12b48gT4sTt-tDn8ufBq9hT-VTVEAbYQbwLLZnDt2iJU/edit#gid=263790710")

# Chargement des noms de pays en français
ref <- gsheet2tbl("https://docs.google.com/spreadsheets/d/1sPNet_GHXm14YEAWqM0zSTR9c4bpa0z4CaJ_ajeWKq8/edit#gid=0")
ref <- select(ref, ISO, nameFra)

# Concaténation des deux tableaux de données
df <- left_join(df, ref, by = "ISO")

# Renommer la colonne nameFra
names(df)[ncol(df)] <- "Origine des dépôts"

# Sélection des dernières années
n_5 <- ncol(df)-1
n_1 <- ncol(df)-11
df <- subset(df, select=c(ncol(df), n_5:n_1))

# Création du tableau
sticky_style <- list(position = "sticky", left = 0, background = "#fff", zIndex = 1,
                     borderRight = "1px solid #eee")

reactable(na.omit(df), 
          searchable = TRUE, 
          highlight = TRUE,
          striped = TRUE,
          showPageSizeOptions = TRUE, 
          pageSizeOptions = c(6, 10), 
          defaultPageSize = 6,
          defaultSortOrder = "desc", 
          defaultSorted = "2020", 
          columns = list(
            `Origine des dépôts` = colDef(
              minWidth = 140,
              style = sticky_style,
              headerStyle = sticky_style)))

Initialement, seuls existaient les systèmes nationaux de brevets, avec pour conséquence une duplication des tâches des offices des brevets (en effet, dans différents pays, ce sont souvent les mêmes éléments de l’état de la technique et les mêmes arguments qui sont invoqués pour mettre en cause la validité des demandes de brevet et en imposer la limitation au cours des procédures officielles d’examen). Il en résultait également des coûts accrus pour les déposants.

L’idée d’un «brevet mondial» ou d’une reconnaissance mutuelle entre différents pays étant peu envisageable, c’est ainsi que s’est développé le système du brevet européen, permettant, par le dépôt et l’examen d’une unique «demande de brevet européen», d’obtenir la délivrance d’un «brevet européen» pouvant exercer ses effets dans un certain nombre de pays européens (« pays désignés ») : le déposant peut désigner n’importe lequel des (actuellement) 31 États contractants. Le brevet européen peut également prendre effet, à compter de la délivrance, dans des États non contractants, au nombre de cinq, qui reconnaissent la validité du brevet délivré dans ces États. Ce système, administré par l’OEB, présente cependant deux inconvénients. Premièrement son coût, trois fois supérieur à celui d’un brevet américain, et ce, en raison principalement de l’obligation imposée par la plupart des pays concernés (et non par la Convention sur le brevet européen) de traduire intégralement un brevet européen, après sa délivrance, dans la (une) langue nationale du pays. Deuxièmement, après la délivrance d’un brevet européen, celui-ci éclate en un «faisceau» de brevets nationaux dans les pays désignés. Ces brevets nationaux mènent alors (classiquement) des vies totalement indépendantes les unes des autres, avec la conséquence notamment qu’en cas de contrefaçon dans plusieurs pays, il est généralement nécessaire d’intenter des actions judiciaires parallèles dans chacun de ces pays, sans aucune certitude cependant quant à l’uniformité des décisions qui seront rendues. Il en résulte donc un accroissement des coûts et de l’incertitude juridique. Avec plus de 160 000 dépôts par an, le système du brevet européen est cependant un grand succès, malgré ses imperfections.

Aux États-Unis, depuis 1860, le nombre de brevets déposés auprès du United States Patent and Trademark Office (USPTO 2020)a augmenté de façon exponentielle (fig.8.5).

D’autres systèmes de brevets régionaux (au sens de région du monde) existent, notamment le brevet eurasien et deux systèmes africains [Organisation africaine de la propriété intellectuelle (OAPI) et African Regional Intellectual Property Organization (ARIPO)].

À l’international, comptant plus de 100 États membres comme on l’a vu précédemment, l’OMPI a développé le système PCT permettant, à travers le dépôt d’une seule «demande internationale», d’obtenir une protection provisoire durant une trentaine de mois : la date de dépôt de la demande PCT vaut comme date de dépôt pour tous les pays désignés dans cette demande. Durant cette période, une recherche préliminaire et un examen préliminaire sont exécutés, ce qui permet au déposant de se faire une meilleure idée quant à la brevetabilité de son invention. Aucun brevet international n’est cependant délivré à l’issue de cette «phase internationale»; si le demandeur souhaite toujours obtenir un brevet dans certains des pays désignés dans la demande initiale, il devra engager la «phase nationale» dans chacun de ceux-ci, selon les procédures respectives. Ce n’est qu’à l’issue de ces procédures nationales que des brevets nationaux (ou éventuellement régionaux, par exemple un brevet européen) pourront être délivrés, avec éventuellement des portées différentes (en fonction des règles nationales).

Pour en revenir à l’Europe, diverses tentatives ont visé la création d’un brevet communautaire (initialement sous la forme d’un système intergouvernemental, dernièrement sous la forme d’un système communautaire). Ce brevet communautaire présenterait l’avantage notable d’être unitaire y compris après sa délivrance, ce qui permettrait la résolution centrale des litiges, avec une certitude juridique nettement plus élevée que dans le système actuel du brevet européen. La négociation (au niveau du Conseil) de la proposition de Règlement de la Commission se heurte cependant à des objections purement politiques de certains pays, notamment sur le plan des exigences de traduction (malgré l’approbation très large des utilisateurs potentiels), et rien ne permet de prévoir quand un brevet communautaire pourrait finalement être disponible.

La Convention de Paris pour la protection de la propriété industrielle (20 mars 1883) ou Convention d’Union de Paris (CUP) a instauré entre les États contractants une union, et elle prévoit que tout ressortissant d’un État contractant jouit des mêmes droits en matière de propriété industrielle qu’un national dans tout autre État de l’Union. Ainsi un inventeur/déposant belge jouit devant le United States Patent and Trademark Office (USPTO) américain des mêmes droits qu’un Étasunien. Et réciproquement en Belgique; car la Belgique et les États-Unis font partie de la CUP, comme actuellement 169 États.

La CUP prévoit également un délai d’un an, dit « délai de priorité », pour permettre à un déposant qui a effectué un premier dépôt régulier dans un pays de l’Union d’effectuer des dépôts pour la même invention dans d’autres États contractants. Ces dépôts ultérieurs seront considérés comme déposés le jour du dépôt de la première demande. Ce premier dépôt s’appelle le «dépôt prioritaire», et sa date, la « date de priorité ». Pour revendiquer par exemple en France la priorité d’un premier dépôt belge, le déposant indique le pays, le numéro du dépôt initial ainsi que la date de priorité.

On dit que ces demandes ultérieures bénéficient d’un droit de priorité vis-à-vis d’éventuelles autres demandes qui pourraient avoir été déposées après la date de priorité par d’autres personnes pour la même invention. On ne pourra pas non plus opposer à ces demandes ultérieures des publications postérieures à la date de priorité. En effet, on doit se placer, pour apprécier la nouveauté et l’activité inventive d’une demande ultérieure sous priorité, à sa date de priorité.

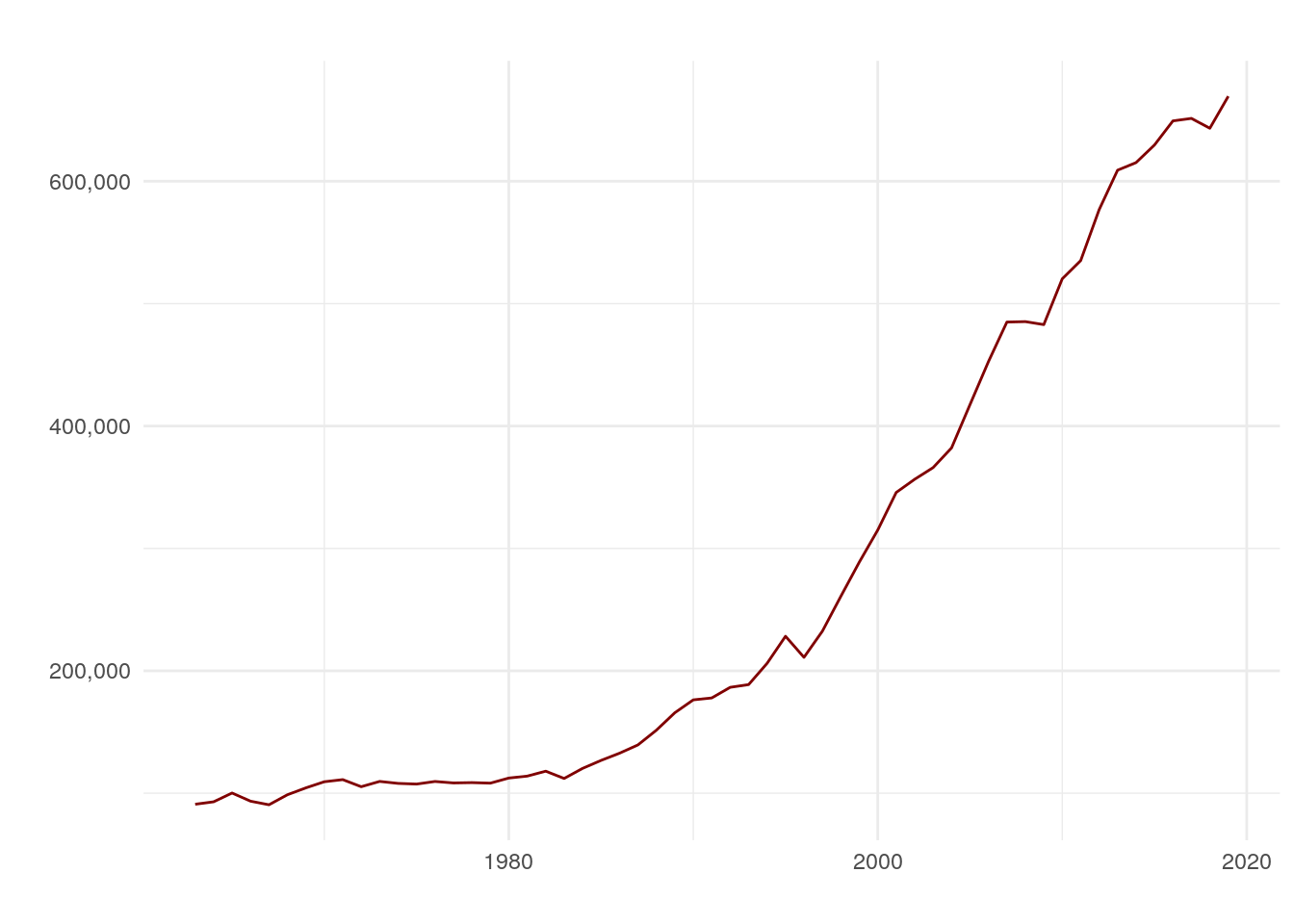
Figure 8.5: Nombre de demandes brevets déposés aux États-Unis par année

Source: USPTO. U.S. Patent Statistics Chart.

[code]

# Chargement des packages
library(rvest)
library(ggplot2)
library(ggsci)

# L'url des données
url <- "https://www.uspto.gov/web/offices/ac/ido/oeip/taf/us_stat.htm"

# Lecture de l'url pour mettre sous forme de tableau
df <- url %>%
  read_html() %>%
  html_nodes('table') %>%
  html_table() 
df <- df[[1]]

# Sélection des colonnes 1 et 8
dt <- df[,c(1,8)]

# Nettoyage des données
dt$`Total Patent Applications *`<- gsub(",", "", dt$`Total Patent Applications *`)
dt$`Total Patent Applications *` <- as.numeric(dt$`Total Patent Applications *`)
dt$country <- "Total"

# Création du graphique
ggplot(data=dt, aes(x=`Year of Application or Grant`, y=`Total Patent Applications *`, color = country)) +
  geom_line()+
  xlab("") + 
  ylab("") +
  ggtitle("") +
  theme_minimal() + 
  theme(legend.position="none") +
  scale_color_uchicago() + 
  scale_y_continuous(labels = scales::comma)

Poursuites juridiques dans le domaine des téléphones intelligents (Adapté de Masnick 2010)

La condamnation de Samsung en août 2012 a initialement abouti à une décision d’un milliard de dollars en faveur d’Apple, ce qui a provoqué une longue série d’appel et un éventuel règlement en 2018. Cette longue bataille légale n’est que le reflet d’une situation où la plupart des entreprises sont en cours de litige. Outre les producteurs de téléphones intelligents, les entreprises doivent faire face aux entités dont la principale source de revenu provient de conflits juridiques par rapport à la propriété intellectuelle (péjorativement appelées en anglais patent trolls). Un tel cas est la bataille prolongée d’Apple avec VirnetX: en février 2020, la Cour Suprême a rejeté l’appel d’Apple, qui tentait d’éviter de payer $440 millions (USD) au prétendu “patent troll”. Le tout offre un paysage juridique pour le moins … complexe.

Source : Kastrenakes 2018, Chung 2020 et Statt 2018

8.3.2 Durée optimale des brevets

En l’absence d’une législation sur les brevets, l’innovation existe incontestablement dans une des trois dimensions définies précédemment. Les brevets ne font pas l’innovation.Enrevanche,il sont très certainement une incidence sur l’innovation, et plus précisément sur les dépenses en RD.

La durée des brevets peut avoir des effets contradictoires. Trop courts, ils n’incitent pas à l’innovation ; trop longs, ils dissuadent les entreprises bénéficiant de brevets de se lancer dans de nouvelles dépenses en RD.

Dans son livre fondamental sur l’invention et le bien-être social, Nordhaus (1969) développe un modèle dans lequel la durée des brevets détermine la taille de l’innovation (voir aussi Levin (1988)). Horowitz et Lai (1996) expliquent que des durées de brevets plus longues augmentent la taille des innovations (les montants investis en RD par exemple), mais diminuent la fréquence des innovations. Gilbert and Shapiro (1990) avaient déjà trouvé un résultat similaire, expliquant que l’importance des innovations s’ajustait à la longueur du brevet.

Horowitz et Lai (1996) représentent l’innovation comme un mouvement le long d’une échelle symbolisant la qualité d’un produit. Une position plus haute sur l’échelle est associée à une meilleure qualité du produit. Ces auteurs définissent la taille de l’inno- vation comme la distance parcourue sur cette échelle, et la fréquence de l’innovation comme le nombre moyen d’innovations par période.

Dans le modèle de Horowitz et Lai (1996), le coût marginal de l’innovation est noté \(c\) et est supposé constant. Dès lors, le coût associé à la distance \(d\) est \(C \times d\). Il y a aussi des imitateurs potentiels de l’innovation qui ne pourront imiter qu’après la période du brevet, notée \(τ\). Ainsi, si l’innovateur développe une innovation à la période t, les imitateurs pourront la produire à la période \(t + \tau\). Le coût de l’imitation est supposé nul. Le coût unitaire de production (distinct des coûts de l’innovation = RD) est constant et noté η. De plus, \(t = [−1, 0, 1, 2 ...[\) où \(t = −1\) représente une technologie préexistante, et \(t = 0\) représente la période à partir de laquelle l’innovation peut apparaître. La position du produit de meilleure qualité à la période \(t\) est notée \(n_t\), \(p\) est le prix du produit et \(x\) est la quantité achetée par les consommateurs. La position sur l’échelle du produit le plus avancé qui peut être imité à la période \(t\) est notée \(m_t\). \(\phi\) va représenter le positionnement en terme de différenciation verticale. Nous faisons l’hypothèse que \(\phi > 1\).

Dans ces conditions, l’entreprise innovante à la position \(n\) produit à un prix:

\[\begin{equation} p_n = \beta \times \phi^{n–m} \tag{8.5} \end{equation}\]

Le prix le plus bas auquel l’imitateur vendra son produit à la position \(m\) sera \(p_m = η\). En adoptant une stratégie de prix limite, l’entreprise innovante capture tout le marché, et l’utilité marginale (\(\mu\)) par dollar pour le bien à la position \(n\) est supérieure à celle pour le bien à la position \(m\):

\[\begin{equation} \frac{\mu_n}{p_n} = \frac{\phi^n}{\beta \times \phi^{n-m}} => \frac{\mu_m}{p_m} = \frac{\phi^m}{\beta} \tag{8.6} \end{equation}\]

Le revenu net de l’entreprise innovante à la période \(t\) est donc:

\[\begin{equation} \pi_{t} = \left( p_{n}-\beta \right) \times x_{n} = \left( p_{n} - \frac{p_{n}}{\phi^{n-m}} \right) \times x_{n} = \left( 1-\frac{1}{\phi^{n-m}} \right) \times p_{n} \times x_{n} \tag{8.7} \end{equation}\]

La description de la menace d’imitation peut être représentée par:

\[\begin{equation} \left\{\begin{matrix} {m_t} = 0 & 0 \leq t < \tau \\ {m_t} = {n_{1-\tau}} & t \geq \tau \end{matrix}\right. \tag{8.8} \end{equation}\]

Après que le brevet a expiré, la position de l’imitateur est celle que l’entreprise innovante occupait \(τ\) périodes plus tôt, c’est-à-dire \(n_{1 – τ}\)

L’entreprise innovante va chercher à maximiser la valeur présente du flux de revenus nets représenté par l’équation précédente :

\[\begin{equation} \max_{{\left \langle n(t) \right \rangle}_{\tau =0}^{\infty}} \sum_{t=0}^{\infty} {\delta}^t\left [ {\pi}_t (n_t, m_t) - C[n_t - n_{t-1}] \right ] \tag{8.9} \end{equation}\]

où \(\delta\) est le facteur d’actualisation \((0 < \delta < 1)\).

Les conditions de premier ordre par rapport à \(n_t\) sont:

\[\begin{equation} \delta^t \times \frac{\partial\pi_t}{\partial n_t}+\delta^{t+\tau} \times \frac{\partial\pi_{t+\tau}}{\partial n_t}-(C \times \delta^t+C\times\delta^{t+\tau}) = 0 \tag{8.10} \end{equation}\]

En insérant l’équation (8.7) dans l’équation (8.10), on obtient:

\[\begin{equation} \left [ \phi^{m_t-n_t} - \delta^\tau\times\phi^{n_t-n_{t+\tau}} \right ] \times p_n\times x_n\times\ln\phi=C\times \left [ 1-\delta \right ] \tag{8.11} \end{equation}\]

En d’autres termes, le revenu marginal de l’innovation \(n_t\) est égal au coût marginal. À partir de l’équation (8.8) pour \(t ≥ τ\), l’équation précédente peut se réécrire:

\[\begin{equation} \phi^{n_{t-\tau}-n_t} = \frac{C\times(1-\delta)}{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi} \tag{8.12} \end{equation}\]

L’entreprise innovante a un programme de RD qui consiste à introduire de nouveaux produits chaque fois que le brevet précédent expire. La taille de l’innovation – donc la taille de l’investissement en RD – peut être mesurée par:

\[\begin{equation} n_t-n_{t-\tau}=\frac{1}{\ln\phi}\times\ln[\frac{(1-\delta^\tau)\times p_n\times x_n\ln\phi}{C\times(1-\delta)}] \tag{8.13} \end{equation}\]

Puisque \(0 < \delta < 1\), la taille de l’investissement augmente avec la durée du brevet. Aussi, une innovation de taille constante apparaîtra toutes les \(τ\) périodes : \([0, τ, 2τ, 3τ, ...]\).

La fréquence de l’innovation peut être définie comme étant \(1/τ\).

Le taux d’innovation, noté \(z\), peut être défini comme suit :

\[\begin{equation} \omega_1 = \frac{(n_t-n_{t-\tau})}{\tau} \tag{8.14} \end{equation}\]

En insérant l’équation (8.14) dans l’équation (8.12), on obtient :

\[\begin{equation} \phi^{-z\times\tau}=\frac{C\times(1-\delta)}{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi} \tag{8.15} \end{equation}\]

On peut alors en extraire le taux d’innovation en fonction des coûts, des fréquences et des facteurs d’actualisation :

\[\begin{equation} \omega_1 = \ln[\frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)}] \times \frac{1}{\tau\times\ln\phi} \tag{8.16} \end{equation}\]

Ainsi, une augmentation de la durée de protection du brevet \(τ\) diminue la fréquence de l’innovation, ce qui a une influence négative sur le taux d’innovation.

Il y a une condition nécessaire: \((1 - \delta^\tau) \times p_n \times x_n \times \ln \phi > C \times (1 - \delta)\).

Il est possible de déterminer le maximum du taux d’innovation en fonction de la durée de protection du brevet :

\[\begin{equation} \tag{8.17} \end{equation}\]

\[\begin{equation} \tag{8.18} \end{equation}\]

Dès lors, il existe un seul \(τ^*\) positif tel que⁶¹

\[\begin{equation} \frac{\partial \omega_1}{\partial t} = - \frac{1}{\tau^2 \times \ln\phi}\times \ln[\frac{(1-\delta^\tau) \times p_n \times x_n \times \ln\phi}{C \times (1-\delta)}] - \frac{\delta^\tau \times \ln\delta}{1-\delta^\tau})=0 \tag{8.19} \end{equation}\]

Preuve

\[ \omega_1 = \ln [\frac{p_n \times x_n \times \ln \phi}{C \times (1 - \delta)} - \frac{p_n \times x_n \times \ln \phi}{C \times (1 - \delta)} \times \delta^\tau] \times \frac{1}{\tau\times\ln\phi} \]

Définissons :

\[ u(\tau) = \ln [\frac{p_n \times x_n \times \ln \phi}{C \times (1 - \delta)} - \frac{p_n \times x_n \times \ln \phi}{C \times (1 - \delta)} \times \delta^\tau] \]

\[ \frac{\partial u}{\partial \tau} = \frac{-p_n \times x_n \times \ln \phi \times \delta^\tau \times \ln \delta / (C \times (1 - \delta))}{(1 - \delta^\tau) \times p_n \times x_n \times \ln \phi} / (C \times (1 - \delta)) \]

\[ \frac{\partial u}{\partial \tau} = - \frac{\delta ^\tau \times \ln \delta}{(1 - \delta ^\tau)} \]

\[ \frac{\partial \omega_2}{\partial t} = - \frac{\delta ^\tau \times \ln \delta}{(1 - \delta ^\tau)} \times \frac{1}{\tau\times\ln\phi} - \ln [ \frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times \frac{1}{\tau^2 \times \ln \phi} = 0 \]

\[ \ln [ \frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times \frac{1}{\tau^2 \times \ln \phi} = - \frac{\delta ^\tau \times \ln \delta}{(1 - \delta ^\tau)} \times \frac{1}{\tau\times\ln\phi} \]

\[ \ln [ \frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times \frac{(1 - \delta^\tau)}{\delta^\tau} = - \tau \times \ln \delta \]

\[ \ln [ \frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times (\delta^{-\tau} - 1) = - \tau \times \ln \delta \]

\[ \ln [ \frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times (1 - \delta^{-\tau}) = \tau \times \ln \delta \]

Afin de déterminer \(\tau^*\), nous savons que \(\tau \times \ln \delta\) est une droite passant par l’origine et de pente \(\ln \delta\). Nous analyons la convexité potentielle \(\ln [ \frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times (1 - \delta^{-\tau})\).

Définissons :

\[ y(\tau) = \ln [ \frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times (1 - \delta^{-\tau}) \]

Alors,

\[ \frac{\partial y}{\partial \tau} = - \frac{\delta^\tau \times \ln \delta}{(1 - \delta^\tau)} \times (1 - \delta^{- \tau}) + \ln [ \frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times \ln \delta \times \delta^{-\tau} \]

ce qui nous amène à :

\[ \frac{\partial y}{\partial \tau} = \ln \delta \times ( - \frac{\delta^\tau \times (1 - \delta^{-\tau})}{(1 - \delta^\tau)} + \ln [ \frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times \delta^{-\tau}) \]

then:

\[ \frac{\partial y}{\partial \tau} = \ln \delta \times ( \ln [ \frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times \delta^{-\tau} + \frac{\delta^\tau \times (\delta^{-\tau} - 1)}{(1 - \delta^\tau)}) \]

et finalement :

\[ \frac{\partial y}{\partial \tau} = \ln \delta \times ( \ln [ \frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times \delta^{-\tau} + 1 \]

with

\[ \forall \omega_1 > 0, \frac{\partial y}{\partial \tau} > 0 \]

et avec :

\[ \forall \tau > 0, \frac{\partial^2 y}{\partial \tau^2} > 0 \]

Par conséquent, en raison de la convexité de \(y(\tau)\), il y a un seul \(\tau^*\) qui est positif et pour lequel \(\partial \omega_1 / \partial \tau = 0\). C’est aussi un maximum car \(\tau \rightarrow \infty\) et \(\omega_1 \rightarrow 0\). Aussi, \(\frac{\partial \omega_1}{\partial \tau}>0\) pour un \(\tau\) suffisamment petit. En conclusion, puisque \(\tau^\ast\) est unique, il est donc obligatoirement aussi un maximum.

Nous devons maintenant déterminer \(\omega_1^\ast\), fondé sur \(\tau^\ast\). Nous savons :

\[ \omega_1 = \ln[\frac{(1-\delta^\tau)\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)}] \times \frac{1}{\tau\times\ln\phi} \]

et nous savons, à l’optimum :

\[ \ln [ \frac{(1-\delta^{\tau^\ast})\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times (1 - \delta^{-\tau^\ast}) = \tau^\ast \times \ln \delta \]

À partir de l’équation précédente :

\[ \tau^\ast = \ln [ \frac{(1-\delta^{\tau^\ast})\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times \frac{(1 - \delta^{-\tau^\ast})}{\ln \delta} \]

alors,

\[ \omega_1^\ast = \ln [ \frac{(1-\delta^{\tau^\ast})\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times \frac{1}{\ln [ \frac{(1-\delta^{\tau^\ast})\times p_n\times x_n\times\ln\phi}{C\times(1-\delta)} ] \times \frac{(1 - \delta^{-\tau^\ast})}{\ln \delta}) \times \ln \phi} \]

donc,

\[ \omega_1^\ast = \frac{\ln \delta}{(1 - \delta^{-\tau^\ast}) \times \ln \phi} = - \frac{\ln \delta}{(\delta^{-\tau^\ast} - 1) \times \ln \phi} \]

par conséquent, puisque :

\[ (\delta^{-\tau^\ast} - 1) <=> \frac{1 - \delta^{\tau^\ast}}{\delta^{\tau^\ast}} \]

\[ \omega_1^\ast = - \frac{\delta^{\tau^\ast} \times \ln \delta} {(1 - \delta^{\tau^\ast}) \times \ln \phi} = \frac{\delta^{\tau^\ast} \times \ln \delta} {(\delta^{\tau^\ast} - 1) \times \ln \phi} \]

Finalement, nous validons que :

\[ \omega_1^{\tau^\ast} > 0, \text{ since } 0<\delta<1 \text{ and } \phi>1 \]

De façon peut-être moins austère, ce résultat peut être représenté par le graphique de la figure 8.6.

On peut voir qu’il y a bien une durée optimale des brevets qui va inciter à l’innovation.

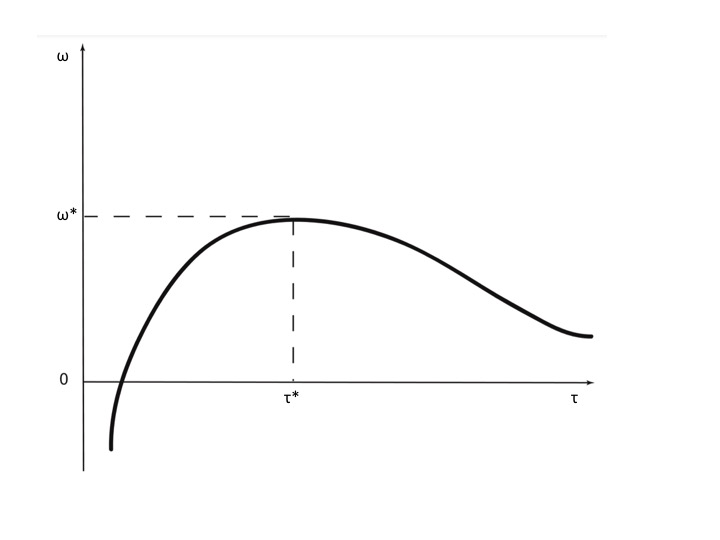
Figure 8.6: Taux d’innovation en fonction de la durée des brevets.

Lerner (2002) va étendre l’analyse de l’innovation à des considérations plus macroéconomiques. Il se livre à une étude des systèmes de protection des droits de propriété intellectuelle dans 60 pays sur une période de 150 années. Il trouve que les pays les plus riches ont plus souvent un système de brevets et permettent aux possesseurs de ces brevets d’en bénéficier plus longtemps. Les pays démocratiques sont aussi dans le même cas de figure.

En ce qui concerne la durée optimale, les économistes sont donc d’accord pour dire qu’il y a une durée optimale de protection des innovations qui va générer le taux maximum d’innovation. Dans la pratique, le \(τ^*\) va dépendre pour chaque pays de l’environnement concurrentiel, des politiques industrielles, etc. Une façon de savoir ce qui est optimal dans un pays est de regarder pendant combien d’années les détenteurs d’un brevet paient les autorités pour conserver ce brevet. En effet, pour maintenir les brevets en vigueur, il faut payer des annuités : le défaut de paiement entraîne la déchéance du brevet. Le tableau 8.4 présente une estimation sur la base du comptage du nombre de brevets ayant fait l’objet d’un paiement d’annuités en 2005.

Table 8.4: Estimation des brevets au 31 décembre 2005

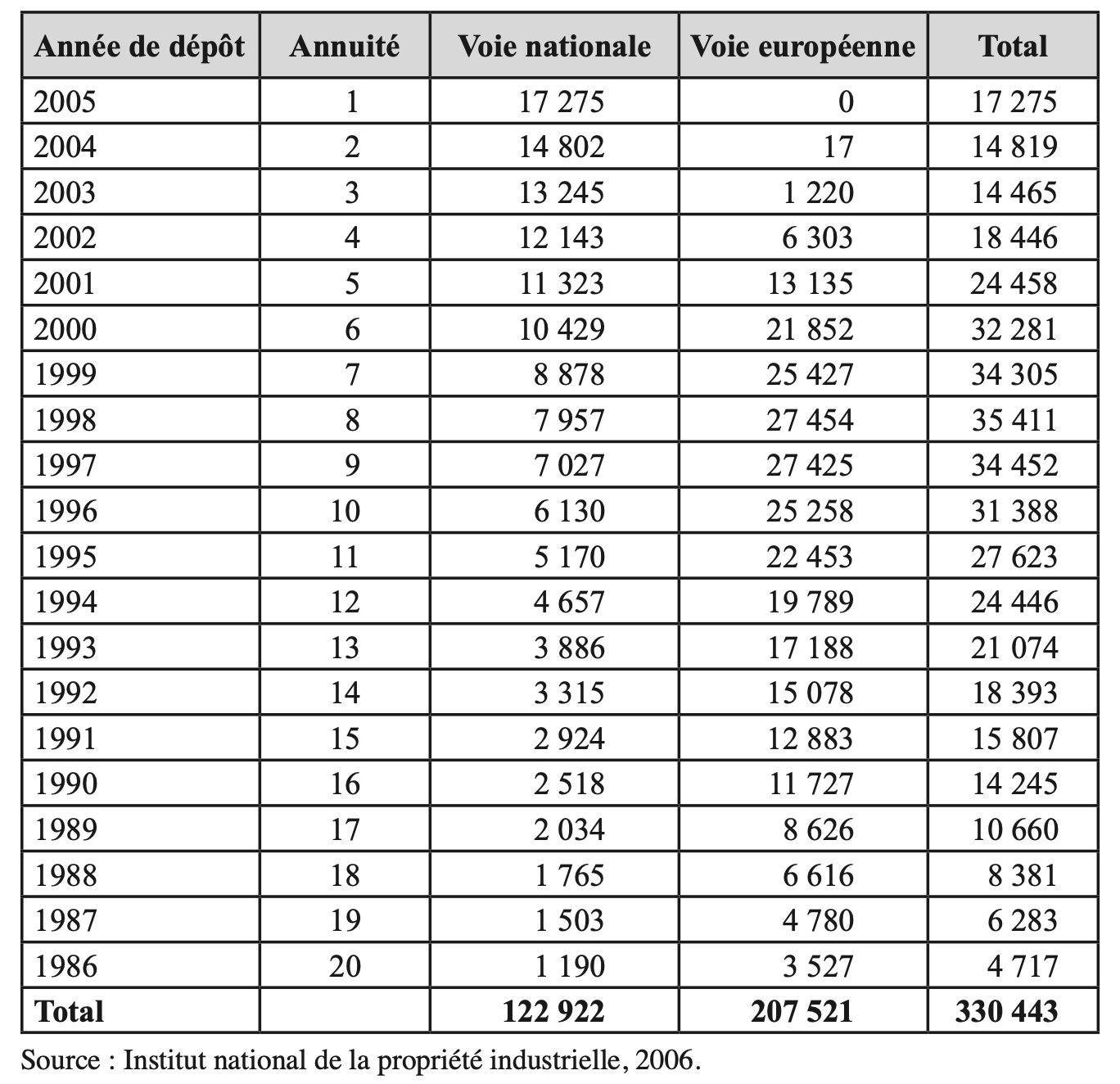La question de la durée des brevets en tant que stratégie prend tout son sens lorsque l’on considère la question de la créativité et son lien avec la croissance économique.

8.3.3 Diffusion de l’innovation : imitation et vente de licences

Mansfield, Schwartz, and Wagner (1981) expliquent qu’en comparaison de la simple imitation d’une innovation, le développement d’une innovation entraîne des coûts moyens d’environ 50 % plus élevés; de plus, il retarde la mise sur le marché du produit créé de 40%. Levin et al. (1987) estiment que le coût de l’imitation d’une innovation est plus élevé pour des produits qui bénéficient de brevets et que le temps de RD requis pour proposer un produit similaire est plus long pour l’imitation de produits brevetés. La protection des brevets confère à une entreprise un avantage concurrentiel dès lors très important (Benoit 1985; Burt 2000; Currie et al. 1999; Gallini 1992; Helpman 1993).

Une façon de réduire les coûts liés à l’imitation d’une innovation est d’acheter des licences. Les ventes de licences d’exploitation d’une innovation existent à la fois dans les pays ayant une législation sur les brevets et lorsqu’il n’y a pas de législation sur les brevets. En effet, beaucoup d’innovations sont difficilement imitables, ou facilement protégeables. Le seul moyen pour une entreprise de bénéficier de l’innovation est alors d’acheter une licence d’exploitation, associée bien souvent à un contrat de service (Dalle 1995). Larson and Anderson (1994) expliquent que les licences d’exploitation participent à partager les risques liés aux dépenses d’investissement. Le rendement de l’investissement est supérieur et les ventes de licences permettent d’investir de nouveau en RD.

Des brevets qui attirent des entreprises (Adapté de Le Monde avec AFP 2012)

En 2012, Google a acheté Motorola Mobility dont le montant avoisinait les 12,5 milliards de dollars, en grande partie motivée par les brevets détenus par le fabricant de téléphones. Google, concepteur du système d’exploitation pour appareils portables Android, souhaitait notamment se protéger contre la concurrence de Microsoft et d’Apple par l’acquisition de ces brevets. L’entreprise a d’ailleurs signé en date du 4 janvier 2012 un contrat avec IBM relativement à l’achat de 188 brevets dans le domaine de la téléphonie mobile. Elle voulait ainsi se munir de moyens pour protéger la place de chef de file de son système d’exploitation pour téléphones intelligents. En 2019, Apple a racheté la majorité des activités d’Intel dans le domaine des modems pour téléphones intelligents. Intel a transféré à Apple 2 200 employés et ces droits de propriété intellectuelle¹. En tenant compte des brevets relatifs aux technologies sans fil nouvellement acquis, au moment de cette transaction Apple détenait plus de 17 000 brevets de technologies sans fil allant des protocoles pour les normes de réseau cellulaire à l’architecture et au fonctionnement des modems. Intel conserva le droit de concevoir des modems pour d’autres applications que les téléphones intelligents, par exemple les ordinateurs personnels, l’Internet des objets et les véhicules autonomes.

---

1. https://www.apple.com/ca/fr/newsroom/2019/07/apple-to-acquire-the-majority-of-intels-smartphone-modem-business/↩︎

8.3.4 Compétition et moment clé de l’innovation

En l’absence d’une législation sur les brevets, et dans le cas d’un duopole, Benoit (1985) explique que si les gains espérés d’une innovation sont importants, l’entreprise rivale peut rapidement imiter l’innovation découverte par l’entreprise innovante. Cela aura pour effet de réduire le rendement de l’investissement de l’innovation. Dans son calcul sur le montant optimal à investir en RD, l’entreprise innovante doit intégrer la fonction de réaction de l’entreprise rivale et doit tenir compte de la possibilité qu’elle puisse être imitée. Si l’innovation est facile à imiter, les investissements seront faibles, et inversement. La structure du marché influe donc sur l’innovation, comme dans le cadre schumpetérien.

Selon Barzel (1968), la concurrence entre innovateurs potentiels pousse les entreprises à surinvestir en RD, ce qui est sous-optimal, car avec un montant moindre, le succès en matière d’innovation serait le même. Barzel (1968) explique également que l’incapacité occasionnelle des innovateurs à retirer tous les bénéfices de l’innovation en raison de la concurrence réduit les montants investis en RD à un niveau sous-optimal pour la société, et plus exactement le taux de croissance de l’économie. De plus, une augmentation de la concurrence a pour effet de pousser les entreprises à rapprocher la date de réalisation de l’innovation, donc à choisir des projets moins ambitieux qui aboutiront plus vite. En effet, elles redoutent de voir un concurrent se lancer dans le même projet de recherche et le réaliser bien avant elles, obtenant ainsi la rente, ou bénéficiant de la protection du brevet (Kamien and Schwartz 1974).

Inspirons-nous du modèle de Barzel (1968) pour déterminer le moment optimal de réalisation d’un investissement. Soit \(r\) le taux d’escompte pour calculer la valeur présente. Soit \(I\) l’investissement nécessaire à l’innovation.

La profitabilité d’une innovation est mesurée par sa valeur présente nette, notée \(R_0\). Elle représente la différence entre les flux de revenus \(S_0\) qui croissent au rythme \(P\) et la valeur présente de l’investissement nécessaire pour cette innovation :

\[\begin{equation} \forall 0 < p < r \end{equation}\]

\[\begin{equation} R_0 = \int_{t}^{\infty} S_0 \times e^{-(r-p)^\tau} d\tau - I \times e^{-rt} \tag{8.20} \end{equation}\]

ce qui amène :

\[\begin{equation} R_0 = \frac{S_0 \times e^{-(r-p)^t}}{r - p} - I \times e^{-rt} \tag{8.21} \end{equation}\]

À partir de l’équation (8.21), on obtient la valeur de \(t\) qui maximise la valeur présente de l’innovation, notée \(t_m\) :

\[\begin{equation} t_m = \frac{\ln r + \ln I - \ln S_0}{p} \tag{8.22} \end{equation}\]

Plus les revenus de l’innovation sont importants et plus le taux de croissance de ces revenus est élevé, alors plus \(t_m\) est faible. Cela signifie que l’innovation doit être réalisée au plus tôt.

À la date \(t_m\), on a, par définition :

\[\begin{equation} S_0 \times e^{-(r-p)^{\times{t_m}}} = r \times I \times e^{-r \times t_m} \tag{8.23} \end{equation}\]

En divisant l’équation (8.23) par \(e^{-r \times {t_m}}\), on obtient :

\[\begin{equation} S_0 \times e^{p \times t_m} = r \times I \tag{8.24} \end{equation}\]

En d’autres termes, le revenu marginal est égal au coût marginal \(r \times I\).

On insère l’équation (8.24) dans l’expression de \(R_0\) (équation (8.21)) :

\[\begin{equation} R_0 = \frac{r \times I \times e^{-r \times t_m}}{r - p} - I \times e^{-r \times t_m} = \frac{p}{r -p} \times e^{-r \times t_m} \tag{8.25} \end{equation}\]

ce qui donne la valeur présente de l’innovation à la période \(t = 0\).

À partir de l’équation (8.25), on peut déterminer la période \(t_z\) pour laquelle la valeur présente nette de l’innovation sera zéro. Ainsi, en posant \(R_0\) égal à 0, on obtient :

\[\begin{equation} t_z = \frac{\ln(r - p) + \ln I - \ln S_0}{p} \tag{8.26} \end{equation}\]

Puisque \(p > 0, t_z < t_m\), le point de valeur présente nulle sera atteint plus tôt que le maximum de la valeur présente. Le graphique de la figure 8.7 représente ces résultats.

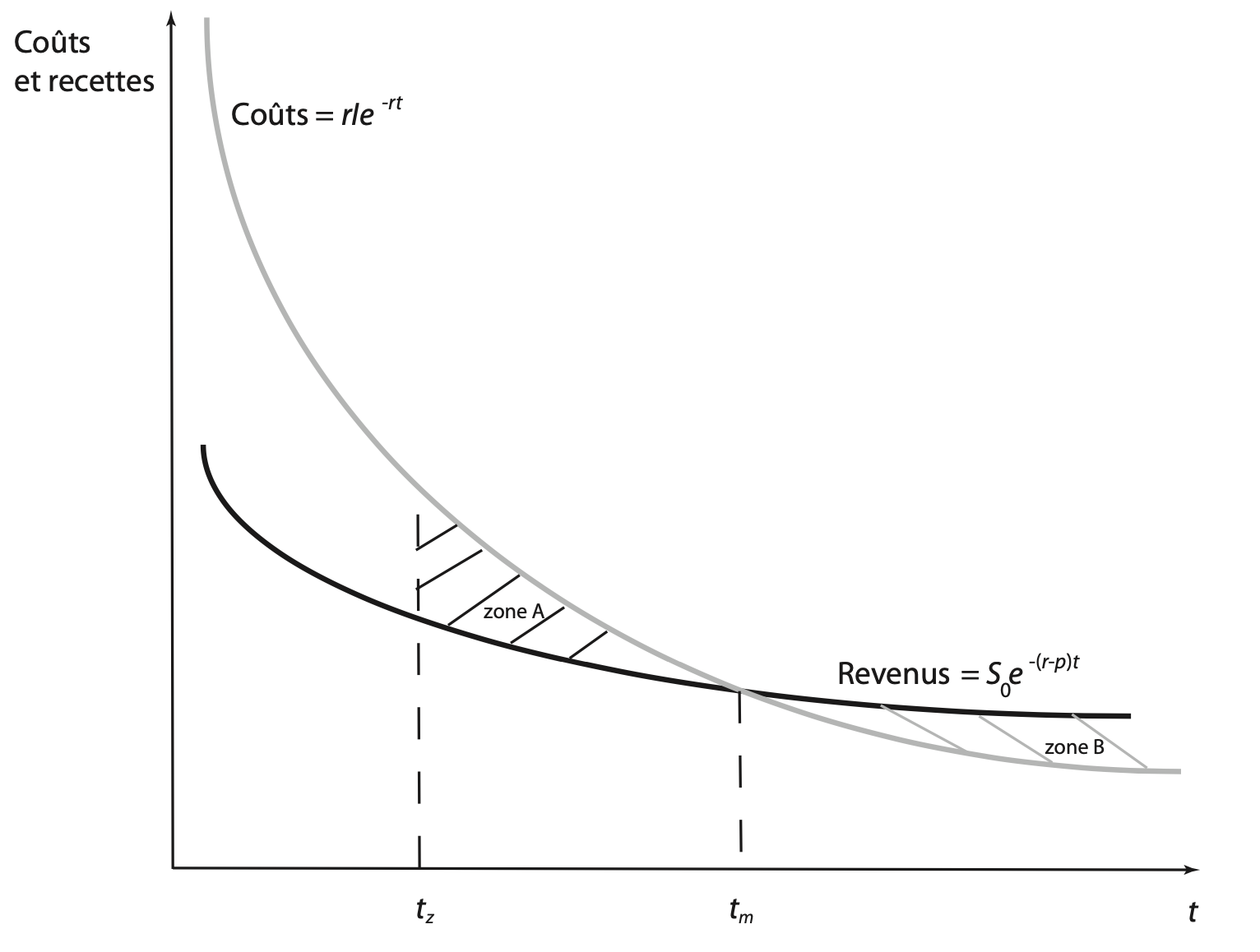
Figure 8.7: Valeur présente nette d’une innovation.

La zone B représente la valeur présente nette de l’innovation. À \(t_m\), le profit est maximum. À \(t_z\), la valeur présente nette est zéro, puisque la valeur présente des pertes entre \(t_z\) et \(t_m\) (représentée par la zone A) est égale à la valeur présente nette au-delà de \(t_m\) (représentée par la zone B). Par conséquent, si une innovation est introduite entre \(t_z\) et \(t_m\), même si la valeur présente n’est pas maximisée, elle est néanmoins positive.

Dès lors, une entreprise en situation dominante ou en monopole introduira l’innovation à la période \(t_m\). En revanche, toute situation concurrentielle conduira les entreprises à essayer d’être les premières à innover. En effet, seule la première obtient les flux de revenus générés par l’innovation. En conséquence, l’équilibre final sera \(t_z\), où les profits sont nuls. Les innovations choisies par une structure de marché concurrentielle seront des innovations qui peuvent être réalisées très rapidement, et seront probablement plus incrémentales que radicales.

Dans le même esprit, Fethke and Birch (1982) ajoutent à la littérature une analyse intégrant le risque de voir des investissements ne menant pas à un résultat probant. Ils concluent que plus le risque d’échec est grand, plus il est tentant d’investir dans des innovations à court terme lorsque la pression concurrentielle est forte.

Bond and Samuelson (1987), quant à eux, démontrent que l’entreprise en situation de monopole qui produit un bien durable a une incitation à investir des ressources en RD dépassant le niveau socialement optimal, récusant les analyses selon lesquelles l’entreprise dominante ou en situation de monopole n’a pas d’incitation à l’innovation. C’est la notion d’efficacité-X (X-efficiency) de Leibenstein (1966) appliquée à l’innovation ou les conclusions de Kamien and Schwartz (1975). L’année suivante, Kamien and Schwartz (1976) viennent en fait raffiner leurs premiers résultats en montrant que des entreprises de grande taille – fort pouvoir de marché – mais en situation de concurrence avec quelques autres entreprises de grande taille représentent un système amenant à des investissements en RD optimaux. Par exemple, quatre entreprises représentant chacune 25 % de parts de marché seraient dans une configuration optimale.

Bond and Samuelson (1987) expliquent que dans le cas de biens non durables, Kamien and Schwartz (1975) peuvent avoir raison, mais qu’avant toute analyse, il importe de déterminer si l’innovation porte sur des biens durables ou non durables. On pourrait même généraliser ce résultat à des processus durables ou non durables.

8.3.5 Peut-on trop innover ? l’exemple de la cannibalisation

L’apparition d’internet est une étude de cas très intéressante. Internet a été une innovation de rupture. Elle a permis l’apparition de nouveaux marchés, de nouveaux débouchés et de nouveaux processus de production. Elle a aussi donné lieu à la cannibalisation. Il s’agit de la possibilité pour une entreprise de l’«ancienne» économie de voir ses parts de marché se réduire à cause de la réplication de son offre sur un site Internet. Quasiment inexistant auparavant, ce risque a pris de l’ampleur avec Internet⁶².

La dynamique est la suivante : une entreprise s’aperçoit de la possibilité de subir la concurrence de nouveaux entrants. La particularité de ces derniers est qu’ils ne vont pas s’opposer sur le même marché – l’ancienne économie – mais s’installer sur Internet. L’entreprise en place prend conscience que son offre a une véritable utilité si elle est aussi diffusée sur Internet, ce qui renforce l’idée que les entrants réussiront à lui faire perdre des parts de marché. La stratégie incontournable est donc d’assurer, elle aussi, une présence sur Internet.

C’est un cas typique d’illustration de la théorie des jeux. Si l’entreprise en place entre sur Internet, elle diminue la probabilité de voir de nouveaux entrants utilisant le même média. En effet, elle peut capitaliser sur son image de marque et capter l’essentiel des internautes. Toutefois, le consommateur peut préférer consulter le site de l’entreprise, offrant par ailleurs d’autres avantages comme celui de l’archivage. Les parts de marché diminueront, cette fois, non pas à cause de l’occupation d’une partie du marché par des entrants, mais par la présence de l’entreprise elle-même sur Internet. Dans ce cas, l’entreprise fait le calcul suivant : dans tous les cas, elle perd des parts de marché sur son marché primaire. Si elle ne fait pas d’offre sur Internet, des entrants risquent de créer une marque et de finir par capter l’ensemble des con- sommateurs en entrant également à terme sur ce marché primaire. Et, si elle fait une offre sur Internet, elle dissuade à l’entrée sur le marché, mais cela lui coûte en investissement et en perte de recettes sur le marché primaire. Les recettes puisées sur le marché primaire étant plus faibles, il faut que l’entreprise les compense par les recettes provenant d’Internet. Cependant, dans bien des cas, ce que les entreprises appellent improprement leurs «modèles économiques» ne fonctionnent pas sur Internet. Il s’agit véritablement d’un nouveau métier. Et, au sein de grandes structures, l’inertie est forte, liée à des contraintes organisationnelles et humaines. Il n’est pas facile de passer d’un métier à un autre. Le succès du site La Presse+ est un exemple de succès à un moment où les quotidiens au format papier traversent une période des plus difficile.

On observe un phénomène similaire avec les produits de la compagnie Apple. En effet, la sortie du iPhone a coïncidé avec la chute des ventes de ses lecteurs de musique iPod. Ce phénomène de cannibalisation s’est amplifié avec la venue de l’iPad en 2011, moment où la compagnie offrait sur le marché trois appareils permettant d’écouter de la musique. De plus, les ventes d’iPad ont fortement impacté la croissance des ventes des ordinateurs personnels iMac dès la moitié de l’année 2012 (fig. 8.8) (Bare Figures 2013; Cheng 2012; Shilov 2013)

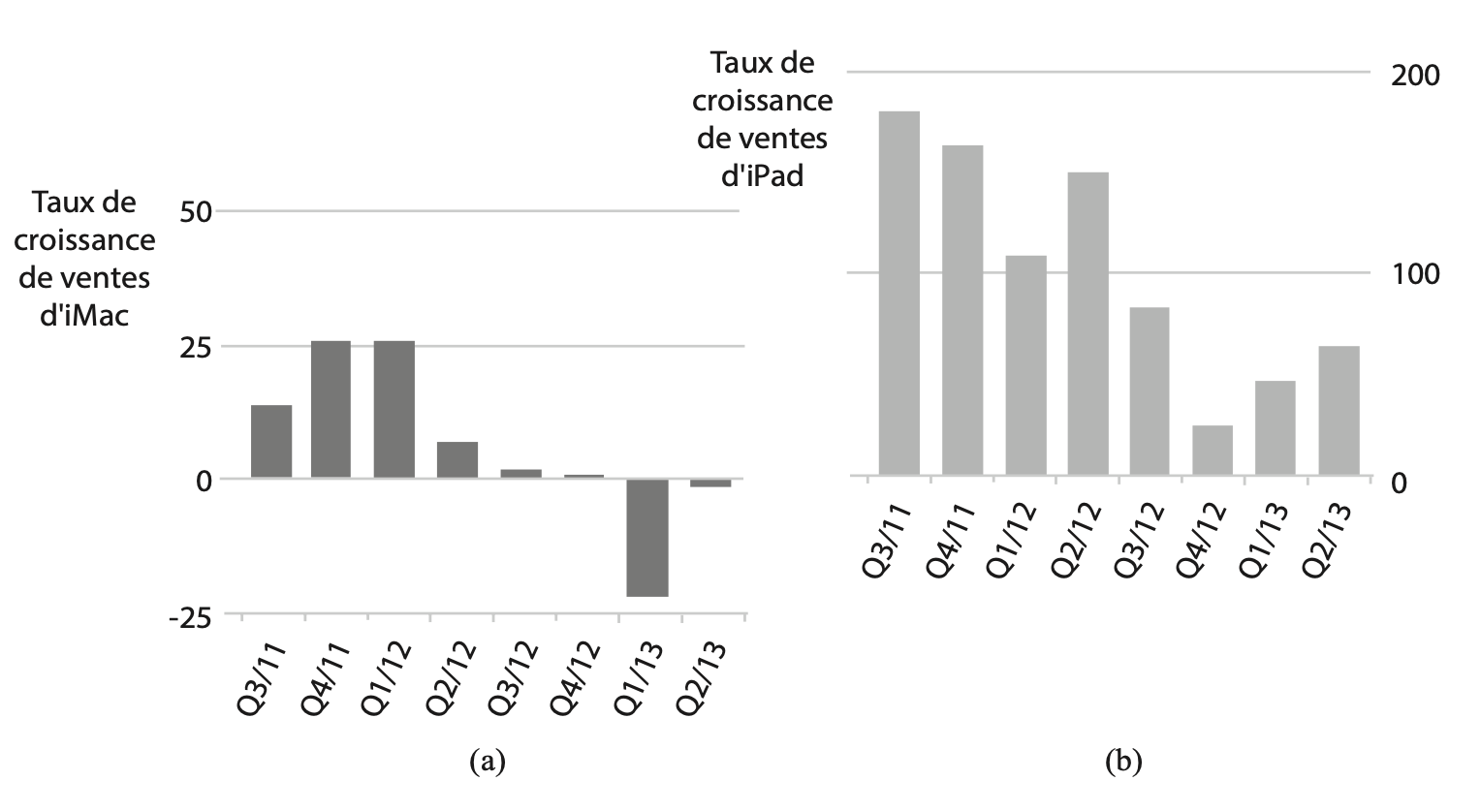
Figure 8.8: Évolution des taux de croissance de ventes : a) iMac ; b) iPad.

8.4 Normes, externalités de réseau, verrouillage technologique et incitations à innover

Les externalités de réseau, les normes et le verrouillage technologique supportent la vision selon laquelle la technologie détermine la structure de marché. Les barrières à l’entrée créées sont toujours importantes et parfois déterminantes pour la survie d’une industrie. Les profits sont souvent monopolistiques, et la notion de concurrence est plus proche de la concurrence monopolistique de E. Chamberlin (1933b) dans sa définition de l’époque que de celle de concurrence imparfaite de Robinson (1933).

8.4.1 Normes et externalités de réseau

Une externalité de réseau apparaît lorsque la plus grande utilisation d’un produit augmente le bénéfice de l’utilisation de ce produit pour tout le monde. Les externalités de réseau sont importantes dans l’analyse des structures de marché parce qu’elles peuvent mener au développement de normes industrielles.

Les normes deviennent une notion importante du fait que les externalités de réseau génèrent des interactions entre les individus et les processus. Les normes peuvent être appréhendées en économie comme des institutions (Glachant 2002). On peut distinguer deux types de normes : normes ouvertes ou fermées, et normes propriétaires ou non propriétaires.

Leica passe au numérique (Adapté de Alix 2006 .)

Dans les années 2000, Leica Camera était le fabricant des «meilleurs» appareils photographiques au monde. Leica Camera avait le leadership en ce qui concerne la qualité de ses optiques, mais aussi des boîtiers à pellicule argentique. En revanche, Leica n’avait aucune division utilisant des composants électroniques. L’entreprise semblait avoir ignoré l’évolution technologique qui s’en venait. L’entreprise allemande, avec une perte, en 2005, de 18,1 millions d’euros sur un chiffre d’affaires annuel de 94 millions d’euros, en baisse de 21% par rapport à l’année 2004, a bien failli déposer le bilan. Néanmoins, l’entreprise s’est adaptée bien plus que ce que l’on pensait… Les nouveaux appareils numérique qu’ils ont proposé pouvaient continuer d’utiliser les optiques des anciens appareils argentiques Leica. Ils ont ainsi essayé de conserver leurs propres clients dans cette transformation.

Les externalités de réseau augmentent la probabilité qu’une industrie devienne monopolistique (Joly 1992). De plus, elles peuvent étendre les pouvoirs de monopole de certaines entreprises (Katz and Shapiro 1992). Le choix entre les normes Blu-ray ou HD-DVD est un exemple moderne de ce qui s’est produit pour le VHS contre la Betacam. Les externalités de réseau peuvent imposer une norme unique – optimale (Betacam) ou sous-optimale (VHS) – alors que plusieurs normes auraient pu exister.

Du point de vue stratégie, dans des secteurs où les normes sont importantes, être le premier à innover procure un avantage concurrentiel indéniable. Il y a une incitation très forte à développer des innovations rapidement, même si elles ne sont pas optimales. Les entreprises peuvent même être désireuses de subir de grosses pertes au tout début afin d’être les premières, puisque ensuite les bénéfices provenant de la norme qu’elles ont imposée seront monopolistiques. Sony a joué cette stratégie en vendant le lecteur DVD Blu-ray à perte.

De plus, les complémentarités (ou les normes) des produits d’entreprises différentes peuvent créer des effets de réseau. Le système d’exploitation de Microsoft, Windows, génère des économies d’échelle avec les autres applications, qu’elles soient produites par Microsoft ou non. Cela entraîne également des barrières à l’entrée, car le nouveau système d’exploitation ne se vendra que si les applications sont écrites pour lui.

8.4.2 Verrouillage technologique

L’innovation semble être un processus qui suit un chemin optimal à chaque période. Optimal et non idéal. « Idéal » voudrait dire qu’il existe un but ultime à l’innovation. Or, considérant les trois composantes de la définition de l’innovation, on comprend bien qu’il n’y a pas un tel but. Peut-être est-ce le cas d’un point de vue technologique et qu’un jour on arrivera aux frontières du réalisable, mais en ce qui concerne l’innovation concurrentielle, elle évoluera sans arrêt. «Optimal» voudrait dire qu’à chaque période, compte tenu des contraintes techniques et organisationnelles, l’innovation est la meilleure qui soit en fonction de ce qui est faisable à cette période donnée. Pourtant en deçà de la version idéale, l’optimalité est loin d’être vraie. L’exemple le plus connu est sans aucun doute la victoire du VHS sur le Betacam quand bien même le Betacam était de qualité supérieure. La raison invoquée dans ce cas de figure est l’importance de la standardisation et les économies de réseau.

Il existe néanmoins, à côté de tout cela, la notion de verrouillage technologique. Une innovation peut être optimale à un moment donné, mais les contraintes technologiques peuvent évoluer et rendre de façon ex post cette innovation sous-optimale. Bien plus, les nouvelles innovations ne peuvent éviter d’utiliser cette première innovation pour des raisons soit de compatibilité – c’est l’exemple des systèmes d’exploitation –, soit de coûts de conversion – c’est l’exemple du clavier QWERTY. On parle alors de verrouillage technologique (path-dependence ou lock-in). Les nouvelles innovations ne seront pas optimales, mais sous-optimales compte tenu des contraintes techniques qui autoriseraient mieux, mais dont les coûts de conversion seraient trop importants. La littérature sur le sujet est abondante avec de nombreux ouvrages de Dopfer (2005), Garrouste, Ioannides, and European Association for Evolutionary Political Economy. (2001), Guinnane, Sundstrom, and Whatley (2004), Tushman and Anderson (2004), ou Nicita and Pagano (2001).

On recense trois catégories de verrouillage technologique:

• la première porte sur la sensibilité au point de départ, mais où il n’y a pas de sous-optimalité. Par exemple, le langage, ou les conventions telles que conduire une voiture du côté droit de la route. Conduire à gauche ne serait pas sous-optimal, ce serait juste une autre forme de convention;

• la deuxième catégorie porte aussi sur la sensibilité au point de départ, mais avec une sous-optimalité ex post, mais pas de sous-optimalité au moment de l’innovation : aucune meilleure décision n’était possible. C’est l’exemple du clavier QWERTY,

• la troisième catégorie porte aussi sur la sensibilité au point de départ avec sous-optimalité ex ante et ex post. En d’autres termes, l’innovation choisie comme point de départ est sous-optimale par rapport à ce qui aurait pu être choisi d’un point de vue technologique. Ce sont les exemples du Betacam contre le VHS, de MS-DOS contre Apple contre DR-DOS (le système d’exploitation de Digital Research), etc.

L’histoire du clavier QWERTY

Christopher Latham Sholes invente le clavier QWERTY en 1868. C’est une nouvelle catégorisation de l’alphabet par rapport au traditionnel et universel (pour le monde occidental) ordre A, B, C, …, Z. Ce clavier est supposé empêcher les bras des touches des machines à écrire de s’entremêler tout en autorisant une frappe suffisamment rapide. Remington produit le premier modèle de machines à écrire Qwerty en 1874. Un concours de vitesse est organisé à Cincinnati en 1888 validant l’utilisation de la séquence QWERTY. De nos jours, alors que les claviers des ordinateurs ne posent plus de problèmes mécaniques, d’aucuns affirment qu’il vaudrait peut-être mieux utiliser la séquence que l’on apprend aux enfants, à savoir A, B, C, …, Z. D’autres séquences ont été proposées, dont celle de Dvorak, brevetée en 1932 (Robinson, 1990).

Maintenant que vous connaissez les différentes incitations à innover, vous pouvez tester vos connaissances en jouant au jeu sérieux «R&D Business Game» hébergé sur nos serveurs ici. Cette app vous donne le rôle du PDG d’une entreprise qui recherche et vend des biens de consommation technologiques pour laquelle vous serez en charge de prendre les décisions d’investissements en terme d’innovation, de marketing ou d’immmitation du concurent.

Figure 8.9: Application R&D Business Game

Le code source est disponible ici : https://github.com/psimm/businessgame

8.5 Innovation et analogies biologiques : innovation ouverte, grappes industrielles, innovation symbiotique et écosystèmes

Devant les nombreux procès auxquels le début des années 2010 a donné lieu, nous sommes en droit de nous poser la question de l’impact du droit de la propriété intellectuelle sur l’innovation. À bien des égards, il semble que la défense de la propriété intellectuelle soit devenue une arme stratégique pour créer des barrières à l’entrée et rester en situation monopolistique. Les entreprises de gros calibre se seraient habituées à vivre dans un environnement dans lequel elles déposent des brevets à tout va, même pour des innovations qui entrent dans des zones grises. Par exemple, les bords ronds de l’iPhone ont permis à Apple de gagner son procès contre Samsung. L’idée de ces dépôts à outrance est que les entreprises plus petites ou qui entrent dans la frange concurrentielle n’auront pas les moyens d’engager un cabinet d’avocats internationaux pour défendre leurs intérêts. Afin d’éviter le risque de payer de fortes amendes, elles préfèrent alors ne pas entrer sur ce marché. La propriété intellectuelle serait donc devenue une barrière à l’entrée stratégique, ce qui la détourne de sa mission première : la protection des inventions, des dessins, des droits d’auteur et de l’image de marque.

8.5.1 Innovation ouverte

La notion d’innovation ouverte s’est développée dans ce contexte. Inspirée de ce qui se passe dans la communauté du logiciel libre, l’idée est que les entreprises puissent collaborer sans se soucier de protéger de petits acquis. Le tout devrait être plus grand que la somme des parties. En collaborant de façon tout à fait transparente, on finirait par avoir un produit ou un service bien supérieur. Évidemment, il y a plusieurs critères à prendre en compte : S’agit-il d’industries naissantes ? S’agit-il de petites entreprises ou de grandes entreprises ? S’agit-il d’entreprises du même secteur industriel ?

Pourtant, dans un contexte international dans lequel la propriété intellectuelle existe, il est difficile de produire en dehors de ces règles sans risquer de donner la technologie à plus fort que soi. De nouveaux modèles se sont donc développés : les développements communs, la création de coentreprises, ou consortiums. L’idée générale est de rassembler les acteurs majeurs, de concevoir et de développer la technologie ensemble, de la breveter, et les droits versés sous forme de licence au consortium seraient reversés à chaque partenaire. Les normes JPEG ou MPEG fonctionnent selon ce système.

8.5.2 Grappes industrielles et innovations symbiotiques

Chère à Porter, une autre forme de développement consisterait à créer des grappes industrielles de nouvelle génération (Porter 1998). Au lieu de rassembler des entreprises du même secteur, on réunirait des entreprises ayant des besoins technologiques similaires. Le consortium en charge de la grappe s’occuperait de gérer la propriété intellectuelle pour les entreprises de la grappe. Ceci correspondrait à une forme d’innovation ouverte non sectorielle avec néanmoins protection de la propriété intellectuelle pour éviter que les plus forts de ce monde ne récupèrent les bonnes idées. De plus, pour le pays qui mettrait en œuvre ce genre de grappes industrielles de nouvelle génération, cela aurait les mêmes effets positifs que les appellations d’origine contrôlée ou le concept de terroir. On pourrait définir ces grappes industrielles de nouvelle génération comme des endroits où les innovations symbiotiques se mettent en place : des entreprises de secteurs différents se réunissent pour développer des innovations utiles à toute la grappe.

8.5.3 Écosystèmes

Les écosystèmes se distinguent des innovations symbiotiques. Il existe plusieurs utilisations du concept d’écosystème dans les médias, à défaut d’avoir une vraie définition. Nous préférons utiliser le concept d’écosystème dans le cas de la stratégie d’une entreprise. Un bel exemple d’un écosystème est Apple. En mettant en place son logiciel iTunes, Apple a permis la centralisation de tous les médias vers un seul logiciel. Il ne lui restait plus qu’à mettre au point différents outils matériels communiquant avec ce logiciel : d’abord, l’ordinateur ; ensuite, le lecteur de musique et de vidéos ; enfin, le téléphone intelligent, et demain, la télévision. iTunes permet aujourd’hui le stockage des données sur le nuage avec iCloud et iTunes Match. Par conséquent, les données sont accessibles en tout temps et peu importe où se trouve l’utilisateur. Cette stratégie de convergence a créé de fortes barrières à l’entrée et a fait en sorte que maintenant, lorsqu’Apple lance un nouveau produit, l’incertitude est faible, car ce nouveau produit se nourrira de l’écosystème. Il est plus facile d’être PDG d’Apple aujourd’hui qu’à ses débuts : Tim Cook gère davantage les finances alors qu’à son époque, Steve Jobs, dans son rôle de PDG, devait d’abord gérer le succès de la mise en place de cet écosystème. C’est la clé du succès d’Apple par rapport à Sony, par exemple. Sony était l’entreprise la plus innovante, une entre- prise que Steve Jobs respectait d’ailleurs. Le problème de Sony : la dissociation entre le logiciel et le matériel. Apple a toujours associé le logiciel et le matériel; c’était la première mise en place du principe de convergence. Dans le monde PC, ce prin- cipe ne s’appliquait pas. Microsoft était en charge des innovations sur le logiciel et les constructeurs se faisaient la concurrence sur le matériel. Très en avance, Sony voulait un logiciel pour gérer tous ses contenus : la musique, les films, etc. La firme japonaise attendait que Microsoft développe ce logiciel. Toutefois, comme Microsoft tardait à le développer (pourquoi innover trop vite quand on est un monopole ?), Sony a décidé de ne pas se laisser distancer par Apple et a lancé son logiciel SonicStage, qui utilisait le format Atrac3 pour les fichiers audio. Il était trop tard pour Sony. MP3 était dominant dans le monde du PC, et Apple allait aussi imposer son format AAC grâce à iTunes et à la capacité d’acheter de la musique en ligne légalement. Sony a subi le contrecoup de la non-convergence entre le logiciel et le matériel. On a beau être une entreprise meneuse dans le matériel, si le logiciel ne suit pas, cela ne sert pas à grand-chose. Laisser l’innovation dans une grande dimension de son entreprise entre les mains d’une autre entreprise est un risque important. Aujourd’hui, Sony est une entreprise comme les autres du monde PC. Elle a perdu tout le capital innovateur qu’elle avait et qui semble se retrouver chez Samsung dans le monde PC aujourd’hui.

Financement de l’innovation version 2.0

Les inventeurs et entrepreneurs disposent de nouvelles plateformes afin d’obtenir les fonds nécessaires à la réalisation de leurs idées. Kickstarter.com est un des nombreux exemples de sites de financement collaboratif (crowdfunding). Depuis 2009¹, 184000 projets ont été financés à partir de plus de 5 milliards de dollars donnés par 18 millions d’internautes.

Les projets les plus variés coexistent sur la plateforme, allant des projets de construction d’imprimante 3D au prototypage de montres intelligentes, jusqu’au financement d’impression de bandes dessinées ou de lancement de CD de musique. Cinq pour cent du financement amassé revient au site, qui offre en contrepartie les facilités de paiement grâce à un partenariat avec Amazon (qui prend 3 à 5 % du montant final).

Les internautes voulant parrainer un projet se voient remettre des récompenses selon leur niveau de participation : cartes postales, t-shirts, livraison à domicile du produit, rencontre avec les fondateurs du projet… Ceci permet aux inventeurs de se concentrer sur la campagne marketing de leur projet, notamment à travers les médias sociaux, afin d’atteindre le montant nécessaire pour obtenir les fonds confiés.

---

1. https://www.kickstarter.com/help/stats↩︎

8.5.4 Innovation et obsolescence programmée

On reproche souvent aux entreprises de manipuler les consommateurs en leur vendant un produit avec la promesse d’une amélioration future. À quel point les mises à jour des produits dépendent-elles de considérations et de contraintes techniques, ou de contraintes de coûts, ou de questions purement stratégiques ?

En présence de contraintes techniques ou de contraintes de coûts, on peut comprendre la nécessité pour l’entreprise de vendre son produit sans toutes les caractéristiques dans le but de générer des fonds qui serviront au développement des versions futures. Dans le cas de considérations stratégiques, il y a deux possibilités : soit l’entreprise veut occuper l’espace et empêcher la concurrence de lui prendre des parts de marché et elle offre alors un produit moins complet, soit elle veut vendre deux produits au lieu d’un seul dans un court intervalle de temps. Dans ce dernier cas de figure, ces stratégies sont bel et bien des stratégies reposant sur le principe de l’obsolescence programmée.

La difficulté pour l’analyste est de faire la distinction entre tous ces cas de figure.

8.6 Conclusion

L’innovation est bel et bien un outil stratégique, aussi important que les autres stratégies étudiées dans les chapitres précédents. De plus, l’innovation est reliée à plusieurs autres dimensions : sa durée, les questions de propriété intellectuelle, l’innovation ouverte, l’obsolescence programmée, etc. Dans toutes ces dimensions, la comparaison avec les autres entreprises de l’industrie complique davantage l’analyse.

References

Alix, Christophe. 2006. “Leica Passe Au Numérique Sans Changer d’optique.” Libération.fr. https://www.liberation.fr/futurs/2006/09/25/leica-passe-au-numerique-sans-changer-d-optique_52336.

Arrow, Kenneth J. 1962. “The Economic Implications of Learning by Doing.” The Review of Economic Studies 29: 155–73. http://links.jstor.org/sici?sici=0034-6527%28196206%2929%3A3%3C155%3ATEIOLB%3E2.0.CO%3B2-%23.

Bare Figures. 2013. “Apple.” Bare Figures. https://barefigur.es/companies/apple/.

Barzel, Yoram. 1968. “Optimal Timing of Innovations.” The Review of Economics and Statistics 50: 348–55. http://links.jstor.org/sici?sici=0034-6535%28196808%2950%3A3%3C348%3AOTOI%3E2.0.CO%3B2-Z.

Benoit, Jean-Pierre. 1985. “Innovation and Imitation in a Duopoly.” The Review of Economic Studies 52: 99–106. http://links.jstor.org/sici?sici=0034-6527%28198501%2952%3A1%3C99%3AIAIIAD%3E2.0.CO%3B2-5.

Bond, Eric W., and Larry Samuelson. 1987. “Durable Goods, Market Structure and the Incentives to Innovate.” Economica 54: 57–67. http://links.jstor.org/sici?sici=0013-0427%28198702%292%3A54%3A213%3C57%3ADGMSAT%3E2.0.CO%3B2-U.

Burgelman, Robert A., and Leonard R. Sayles. 1986. Inside Corporate Innovation : Strategy, Structure, and Managerial Skills. New York London: Free Press ; Collier-Macmillan.

Burt, Roger. 2000. “Innovation or Imitation? Technological Dependency in the American Nonferrous Mining Industry.” Technology and Culture 41: 321–47. http://muse.jhu.edu/journals/technology_and_culture/v041/41.2burt.html.

Chamberlin, Edward. 1933b. The Theory of Monopolistic Competition. 1st ed. Harvard Economic Studies. Cambridge: Harvard university press.

Cheng, Roger. 2012. “Apple’s Biggest iPad Rival: The iPhone 4S.” CNET. https://www.cnet.com/news/apples-biggest-ipad-rival-the-iphone-4s/.

Currie, David, Paul Levine, Joseph Pearlman, and Michael Chui. 1999. “Phases of Imitation and Innovation in a North-South Endogenous Growth Model.” Oxford Economic Papers 51: 60–88. http://dx.doi.org/10.1093/oep/51.1.60.

Dalle, Jean-Michel. 1995. “Dynamiques d’adoption, Coordination et Diversite: La Diffusion Des Standards Technologiques.” Revue Economique 46: 1081–98. http://links.jstor.org/sici?sici=0035-2764%28199507%2946%3A4%3C1081%3ADDCEDL%3E2.0.CO%3B2-A.

Dopfer, Kurt. 2005. The Evolutionary Foundations of Economics. Cambridge: Cambridge University Press.

Fethke, Gary C., and John J. Birch. 1982. “Rivalry and the Timing of Innovation.” The Bell Journal of Economics 13: 272–79. http://links.jstor.org/sici?sici=0361-915X%28198221%2913%3A1%3C272%3ARATTOI%3E2.0.CO%3B2-C.

Gallini, Nancy T. 1992. “Patent Policy and Costly Imitation.” The RAND Journal of Economics 23: 52–63. http://links.jstor.org/sici?sici=0741-6261%28199221%2923%3A1%3C52%3APPACI%3E2.0.CO%3B2-S.

Garrouste, Pierre, Stavros Ioannides, and European Association for Evolutionary Political Economy. 2001. Evolution and Path Dependence in Economic Ideas : Past and Present. Cheltenham, UK ; Northampton, MA: Edward Elgar.

Gilbert, Richard, and Carl Shapiro. 1990. “Optimal Patent Length and Breadth.” The RAND Journal of Economics 21: 106–12. http://links.jstor.org/sici?sici=0741-6261%28199021%2921%3A1%3C106%3AOPLAB%3E2.0.CO%3B2-2.

Glachant, Jean-Michel. 2002. “L’approche Neo-Institutionnelle de La Reforme Des Industries de Reseaux.” Revue Economique 53: 425–35. http://links.jstor.org/sici?sici=0035-2764%28200205%2953%3A3%3C425%3ALNDLRD%3E2.0.CO%3B2-I.

Guinnane, Timothy, William Andrew Sundstrom, and Warren C. Whatley. 2004. History Matters : Essays on Economic Growth, Technology, and Demographic Change. Stanford, Calif.: Stanford University Press.

Helpman, Elhanan. 1993. “Innovation, Imitation, and Intellectual Property Rights.” Econometrica 61: 1247–80. http://links.jstor.org/sici?sici=0012-9682%28199311%2961%3A6%3C1247%3AIIAIPR%3E2.0.CO%3B2-C.

Horowitz, Andrew W., and Edwin L.-C. Lai. 1996. “Patent Length and the Rate of Innovation.” International Economic Review 37: 785–801. http://links.jstor.org/sici?sici=0020-6598%28199611%2937%3A4%3C785%3APLATRO%3E2.0.CO%3B2-E.

Hotelling, Harold. 1929. “Stability in Competition.” The Economic Journal 39: 41–57.

Joly, Pierre-Benoit. 1992. “Le Role Des Externalités Dans Les Systemes d’innovation. Nouveaux Regards Sur Le Dilemme de La Proprieté Intellectuelle.” Revue Economique 43: 785–96. http://links.jstor.org/sici?sici=0035-2764%28199207%2943%3A4%3C785%3ALRDEDL%3E2.0.CO%3B2-V.

Jon, Evans. 2012. “Microsoft’s Long and Winding Road to Becoming Kind of Cool.” TechCrunch. https://social.techcrunch.com/2012/11/24/wait-when-did-microsoft-become-kind-of-cool/.

Kamien, Morton I., and Nancy L. Schwartz. 1974. “Patent Life and R and D Rivalry.” The American Economic Review 64: 183–87. http://links.jstor.org/sici?sici=0002-8282%28197403%2964%3A1%3C183%3APLARAD%3E2.0.CO%3B2-6.

Kamien, Morton I., and Nancy L. Schwartz. 1974. “Patent Life and R and D Rivalry.” The American Economic Review 64: 183–87. http://links.jstor.org/sici?sici=0002-8282%28197403%2964%3A1%3C183%3APLARAD%3E2.0.CO%3B2-6.

1975. “Market Structure and Innovation: A Survey.” Journal of Economic Literature 13: 1–37. http://links.jstor.org/sici?sici=0022-0515%28197503%2913%3A1%3C1%3AMSAIAS%3E2.0.CO%3B2-A.

Kamien, Morton I., and Nancy L. Schwartz. 1974. “Patent Life and R and D Rivalry.” The American Economic Review 64: 183–87. http://links.jstor.org/sici?sici=0002-8282%28197403%2964%3A1%3C183%3APLARAD%3E2.0.CO%3B2-6.

1975. “Market Structure and Innovation: A Survey.” Journal of Economic Literature 13: 1–37. http://links.jstor.org/sici?sici=0022-0515%28197503%2913%3A1%3C1%3AMSAIAS%3E2.0.CO%3B2-A.

1976. “On the Degree of Rivalry for Maximum Innovative Activity.” The Quarterly Journal of Economics 90: 245–60. http://links.jstor.org/sici?sici=0033-5533%28197605%2990%3A2%3C245%3AOTDORF%3E2.0.CO%3B2-8.

Katz, Michael L., and Carl Shapiro. 1992. “Product Introduction with Network Externalities.” The Journal of Industrial Economics 40: 55–83. http://links.jstor.org/sici?sici=0022-1821%28199203%2940%3A1%3C55%3APIWNE%3E2.0.CO%3B2-W.

Larson, Bruce A., and Margot Anderson. 1994. “Technology Transfer, Licensing Contracts, and Incentives for Further Innovation.” American Journal of Agricultural Economics 76: 547–56. http://links.jstor.org/sici?sici=0002-9092%28199408%2976%3A3%3C547%3ATTLCAI%3E2.0.CO%3B2-A.

Leibenstein, Harvey. 1966. “Allocative Efficiency Vs. "X-Efficiency".” The American Economic Review 56: 392–415. http://links.jstor.org/sici?sici=0002-8282%28196606%2956%3A3%3C392%3AAEV%22%3E2.0.CO%3B2-O.

Le Monde avec AFP. 2012. “Google Rachète Près de 200 Brevets à IBM.” Le Monde.fr, January. https://www.lemonde.fr/technologies/article/2012/01/05/google-rachete-pres-de-200-brevets-a-ibm_1625818_651865.html.

Lerner, Josh. 2002. “150 Years of Patent Protection.” The American Economic Review 92: 221–25. http://links.jstor.org/sici?sici=0002-8282%28200205%2992%3A2%3C221%3A1YOPP%3E2.0.CO%3B2-0.

Levin, Richard C. 1988. “Appropriability, R&D Spending, and Technological Performance.” The American Economic Review 78: 424–28. http://links.jstor.org/sici?sici=0002-8282%28198805%2978%3A2%3C424%3AARSATP%3E2.0.CO%3B2-5.

Levin, Richard C., Alvin K. Klevorick, Richard R. Nelson, Sidney G. Winter, Richard Gilbert, and Zvi Griliches. 1987. “Appropriating the Returns from Industrial Research and Development.” Brookings Papers on Economic Activity 1987: 783–831. http://links.jstor.org/sici?sici=0007-2303%281987%291987%3A3%3C783%3AATRFIR%3E2.0.CO%3B2-Z.

Libération. 2013. “Une Tablette Tactile Fine Comme Du Papier.” Libération.fr. https://www.liberation.fr/futurs/2013/01/09/une-tablette-tactile-fine-comme-du-papier_872683.

Mairesse, Jacques, and Pierre Mohnen. 2002. “Accounting for Innovation and Measuring Innovativeness: An Illustrative Framework and an Application.” The American Economic Review 92: 226–30. http://links.jstor.org/sici?sici=0002-8282%28200205%2992%3A2%3C226%3AAFIAMI%3E2.0.CO%3B2-K.

Mansfield, Edwin, Mark Schwartz, and Samuel Wagner. 1981. “Imitation Costs and Patents: An Empirical Study.” The Economic Journal 91: 907–18. http://links.jstor.org/sici?sici=0013-0133%28198112%2991%3A364%3C907%3AICAPAE%3E2.0.CO%3B2-X.

Masnick, Mike. 2010. “Meet the Patent Thicket: Who’s Suing Who for Smartphone Patents.” Techdirt. https://www.techdirt.com/articles/20101007/22591311328/meet-the-patent-thicket-who-s-suing-who-for-smartphone-patents.shtml.

Nicita, Antonio, and Ugo Pagano. 2001. The Evolution of Economic Diversity. Routledge Siena Studies in Political Economy. London ; New York: Routledge.

Nordhaus, William D. 1969. Invention Growth, and Welfare; a Theoretical Treatment of Technological Change. M.I.T. Monographs in Economics ; 10. Cambridge, Mass., M.I.T. Press.

Porter, Michael E. 1998. “Clusters and the New Economics of Competition.” Harvard Business Review, nos. November-December 1998 (November). https://hbr.org/1998/11/clusters-and-the-new-economics-of-competition.

Redlich, Fritz. 1951. “Innovation in Business: A Systematic Presentation.” American Journal of Economics and Sociology 10: 285–91. http://links.jstor.org/sici?sici=0002-9246%28195104%2910%3A3%3C285%3AIIBASP%3E2.0.CO%3B2-8.

Robertson, Thomas S. 1967. “The Process of Innovation and the Diffusion of Innovation.” Journal of Marketing 31: 14–19. http://links.jstor.org/sici?sici=0022-2429%28196701%2931%3A1%3C14%3ATPOIAT%3E2.0.CO%3B2-D.

Robinson, Joan. 1933. The Economics of Imperfect Competition. London, Macmillan; Co., ltd.

Roland, Alex. 1977. “Problems of Definition.” Technology and Culture 18: 509–11. http://links.jstor.org/sici?sici=0040-165X%28197707%2918%3A3%3C509%3APOD%3E2.0.CO%3B2-%23.

Schumpeter, Joseph Alois. 1939. Business Cycles; a Theoretical, Historical, and Statistical Analysis of the Capitalist Process. 1st ed. New York, McGraw-Hill.

Shilov, Anton. 2013. “Apple Reports Record Shipments of iPad and iPhone Amid Declines of Mac and iPod Sales.”

Stiglitz, Joseph E., and Partha Dasgupta. 1981. “Market Structure and Resource Extraction Under Uncertainty.” The Scandinavian Journal of Economics 83: 318–33. http://links.jstor.org/sici?sici=0347-0520%281981%2983%3A2%3C318%3AMSAREU%3E2.0.CO%3B2-8.

Tushman, Michael, and Philip Anderson. 2004. Managing Strategic Innovation and Change : A Collection of Readings. 2nd ed. New York: Oxford University Press.

Tushman, Michael L., and Philip Anderson. 1986. “Technological Discontinuities and Organizational Environments.” Administrative Science Quarterly 31 (September): 439–65.

USPTO. 2020. “Issue Years and Patent Numbers.” U.S. Patent and Trademark Office. https://www.uspto.gov/web/offices/ac/ido/oeip/taf/issuyear.htm.

---

57. Ce traité est devenu le Traité sur le focntionnement de l’Union européenne en 2009.↩︎

58. Merci à Charles Grison, étudiant à HEC Montréal, pour son aide dans cette partie. Les erreurs et omissions restent les nôtres.↩︎

59. Les auteurs de la théorie managériale ont largement traité l’aspect non optimal des décisions des managers (par exemple, R. Marris, O. E. Williamson et W. Baumol).↩︎

60. Évidemment, la taille initiale de l’économie canadienne joue aussi un rôle important. Les économies les plus petites ont tendance à être plus ouvertes en pourcentage du PIB.↩︎

61. de Conseil Économique et social (1973)↩︎

62. L’initiateur du paradigme SCP est E. Mason (1939). Quelques années plus tard, J. Bain (1959) va enrichir le modèle de base↩︎

63. Cette commission a été créée en 1914 pour interpréter et faire appliquer les interdictions concernant la concurrence déloyale.↩︎