Chapitre 2 Technologie et processus de production

À retenir

Dans la réalité, la firme est un nœud complexe d’interactions. Pour simplifier, les facteurs de production, qui sont les intrants utilisés dans le processus de production, sont souvent regroupés en grandes catégories : matières premières, machines, énergie, travail, etc. Du point de vue le plus agrégé, les deux seuls facteurs de production sont le capital et le travail. L’étude de différents indicateurs tels que la productivité moyenne ou la productivité marginale va permettre de décider quels intrants choisir, quelle quantité produire, quand arrêter la production et pourquoi il existe une taille optimale à une entreprise.

2.1 Introduction

La science économique comporte une difficulté supplémentaire par rapport à d’autres sciences : elle demande de fournir des représentations du monde qui soient à la fois suffisamment simplifiées pour être compréhensibles et suffisamment sophistiquées pour ne pas limiter les conclusions des analyses. Elle doit modéliser des «particules» (les agents économiques) qui contrôlent leurs trajectoires, qui font des erreurs, qui apprendront de leurs erreurs ou pas, dont on ne sait pas quand elles apprendront de leurs erreurs et qui ont un horizon fini avec une grande variabilité. Appliquée au monde de l’organisation industrielle, la science économique simplifie l’entreprise en proposant une représentation qui s’appuie sur la fonction de production à deux intrants : le capital et le travail. On a donc pour hypothèses soit que l’on garde constants les autres paramètres internes à l’entreprise (par exemple, la gestion des ressources humaines, la commercialisation des produits, etc.), soit que l’on garde constants l’environnement macroéconomique, les forces concurrentielles, etc. Une fois cette fonction de production définie, nous réintégrerons ces différentes dimensions dans l’analyse à travers les chapitres suivants. Dans ce chapitre, nous allons présenter les fondements de l’analyse tels qu’ils ont été développés par les ingénieurs de l’économie de la fin du xixe siècle et du début du xxe siècle. Les mots de Pierre de Jean Olivi, de Jean Bodin, de Turgot, de Bernard de Mandeville, d’Adam Smith ont été transformés en variables par Cournot, Marshall, Edgeworth, Walras, Robinson, Chamberlin et bien d’autres auteurs.

2.2 De l’intrant à l’extrant : la fonction de production et ses déclinaisons

2.2.1 Fonction de production

La firme est positionnée sur un marché. La fonction de demande de ses produits est exogène. La firme connaît le prix de vente et les prix d’achat des intrants, c’est-à-dire le prix des matières premières et le taux de salaire des employés. Pour atteindre son objectif de maximisation du profit, elle dispose d’une multitude de combinaisons possibles de ses intrants.

Connaissant le prix de vente et la demande, l’entreprise peut en inférer la quantité demandée et donc la quantité qu’elle doit elle-même offrir pour maximiser son profit. Mais pour atteindre cette quantité, elle a le choix des facteurs de production. Nul doute qu’une combinaison sera plus efficace que toutes les autres. Par exemple, une rotative d’imprimerie nécessite deux ouvriers; un troisième serait de trop tandis qu’un seul ne permettrait pas, dans le même laps de temps, de produire les mêmes quantités.

Pour offrir une certaine quantité d’extrants, seules certaines combinaisons d’intrants permettent d’atteindre le degré d’efficacité maximal.

La fonction de production pour une firme peut s’écrire (2.1) :

\[\begin{equation} y=f (X_1, ..., X_n) \tag{2.1} \end{equation}\]

où \({(X_1, ..., Xn)}\) sont les quantités des différents facteurs. C’est la fonction de production y qui représente les extrants.

Si l’on simplifie pour deux facteurs, le capital \(K\) et le travail \(L\), la combinaison de ces deux grandes catégories d’intrants peut être représentée par (2.2):

\[\begin{equation} Q=f (K, L) \tag{2.2} \end{equation}\]

On peut représenter l’ensemble de production comme l’illustre la figure 2.1.

Figure 2.1: Représentation de l’ensemble de production et de la fonction de production.

L’ensemble de production permet de décrire l’ensemble de toutes les combinaisons d’intrants qui correspondent à un processus de production techniquement réalisable. La fonction qui décrit la frontière de cet ensemble est appelée «fonction de production»et ne considère que l’extrant maximum possible pour un niveau donné d’intrant.

Cette production dépend donc des décisions de gestion de l’entreprise, approximées par les deux variables représentant les deux intrants : le capital \(K\) et le travail \(L\). Cependant, il y a bien d’autres dimensions à prendre en compte : l’environnement concurrentiel, les diversités culturelles, les héritages nationaux, la force de la mondialisation; bref, des paramètres qu’une entreprise ne peut contrôler, mais avec lesquels elle peut jouer.

Par exemple, la première contrainte à laquelle l’entreprise devra s’ajuster sera sa contribution aux dépenses publiques du pays dans lequel elle a installé son siège social. Cette contribution se fait à travers notamment – et pas seulement – l’impôt sur les bénéfices des sociétés. Le tableau 2.1 présente un indicateur de la contribution : le taux de l’impôt sur les bénéfices des sociétés, qui n’est qu’une approximation du taux d’impôt (il faudrait y ajouter les abattements fiscaux possibles par secteur industriel pour avoir un taux effectif par secteur).

Table 2.1: Taux de l’impôt sur les bénéfices des sociétés dans les pays de l’OCDE en 2020

Pays	Taux de l’impôt sur les bénéfices des sociétés
Australia	30%
Austria	25%
Belgium	25%
Canada	15%
Chile	25%
Denmark	22%
Estonia	20%
Finland	20%
France	32%
Germany	16%
Greece	24%
Hungary	9%
Iceland	20%
Ireland	12%
Italy	24%
Japan	23%
Luxembourg	18%
Mexico	30%
Netherlands	25%
New Zealand	28%
Norway	22%
Poland	19%
Portugal	30%
Slovakia	21%
South Korea	25%
Spain	25%
Sweden	21%
Switzerland	8%
Turkey	22%

Warin, Thierry (2020): OECD R Package: A Use Case. figshare. Dataset. https://doi.org/10.6084/m9.figshare.12928763.v1

[code]

# Chargement des packages
library(OECD)
library(dplyr)
library(formattable)
library(kableExtra)

# Récupération des données de l'OCDE via l'API OECD
corpo_income_taxrate <- get_dataset(dataset = "CTS_CIT")
dt <- filter(corpo_income_taxrate, obsTime == max(corpo_income_taxrate$obsTime))
dt <- filter(dt, CORP_TAX == "CIT_RATE")

# Récupération de la liste des pays de l'OCDE
ref <- gsheet::gsheet2tbl("https://docs.google.com/spreadsheets/d/1sPNet_GHXm14YEAWqM0zSTR9c4bpa0z4CaJ_ajeWKq8/edit#gid=0")
ref <- select(ref, nameEng, ISO3)
ref <- subset(ref, nameEng %in% c("Austria", "Belgium", "Canada", "Denmark", "France", "Germany", "Greece", "Iceland", "Ireland", "Italy", "Luxembourg", "Netherlands", "Norway", "Portugal", "Spain", "Sweden", "Switzerland", "Turkey", "UK", "USA", "Australia", "Finland", "Japan", "New Zealand", "Belgium", "Chile", "Czechia", "Estonia", "Hungary", "Mexico", "Poland", "Slovakia", "South Korea"))
names(ref)[2] <- "COU"

# Nettoyage des données pour un meilleur affichage
dt <- left_join(ref, dt, by = "COU")
dt <- select(dt, nameEng, obsValue)
dt$obsValue <- paste(round(dt$obsValue, digits = 0), "%", sep="")
colnames(dt) <- c("Pays", "Taux de l’impôt sur les bénéfices des sociétés")

# Création du tableau
dt %>%
  kable(align=rep('c', 2), caption = paste0("Taux de l’impôt sur les bénéfices des sociétés dans les pays de l’OCDE en ", max(corpo_income_taxrate$obsTime))) %>%
  kable_styling(c("striped", "bordered")) %>%
  scroll_box(height = "430px")

Dans les chapitres suivants, nous utiliserons pour simplifier les notations et les représentations d’une fonction de production où seul un des deux facteurs de production est variable, l’autre étant fixe. Par exemple, pour être plus proche de la réalité, on supposera que le capital est le facteur fixe, noté \(K_0\). En effet, au moins à court terme, la taille d’une usine est fixe, la taille d’une exploitation agricole est fixe, etc. On obtient représentation de la figure 2.2.

Figure 2.2: Représentation de la fonction de production (avec l’intrant capital fixé à un niveau \(K_0\)).

2.2.2 Productivité moyenne, productivité marginale et rendements d’échelle

À partir de la fonction de production, il est possible de tirer plusieurs enseignements sur la technologie employée dans l’entreprise. L’étude de différents indicateurs tels que la productivité moyenne ou la productivité marginale va permettre de déciderquels intrants choisir, quelle quantité produire, quand arrêter la production, etc.

Pour amorcer la réflexion, l’auteur de l’ouvrage Bailout Nation, Barry Ritholtz (2009), a présenté dans son blogue une analyse intéressante sur la durée de vie moyenne des entreprises d’Internet. Il y indique que cette durée de vie est de 11 ans (fig. 2.3). Le cycle de vie est donc un ensemble fini. À la date de publication de son blogue, Ritholtz (2012) rappelle avec humour que Facebook a «déjà» huit ans d’existence. Aujourd’hui, Facebook a 16 années d’existence.

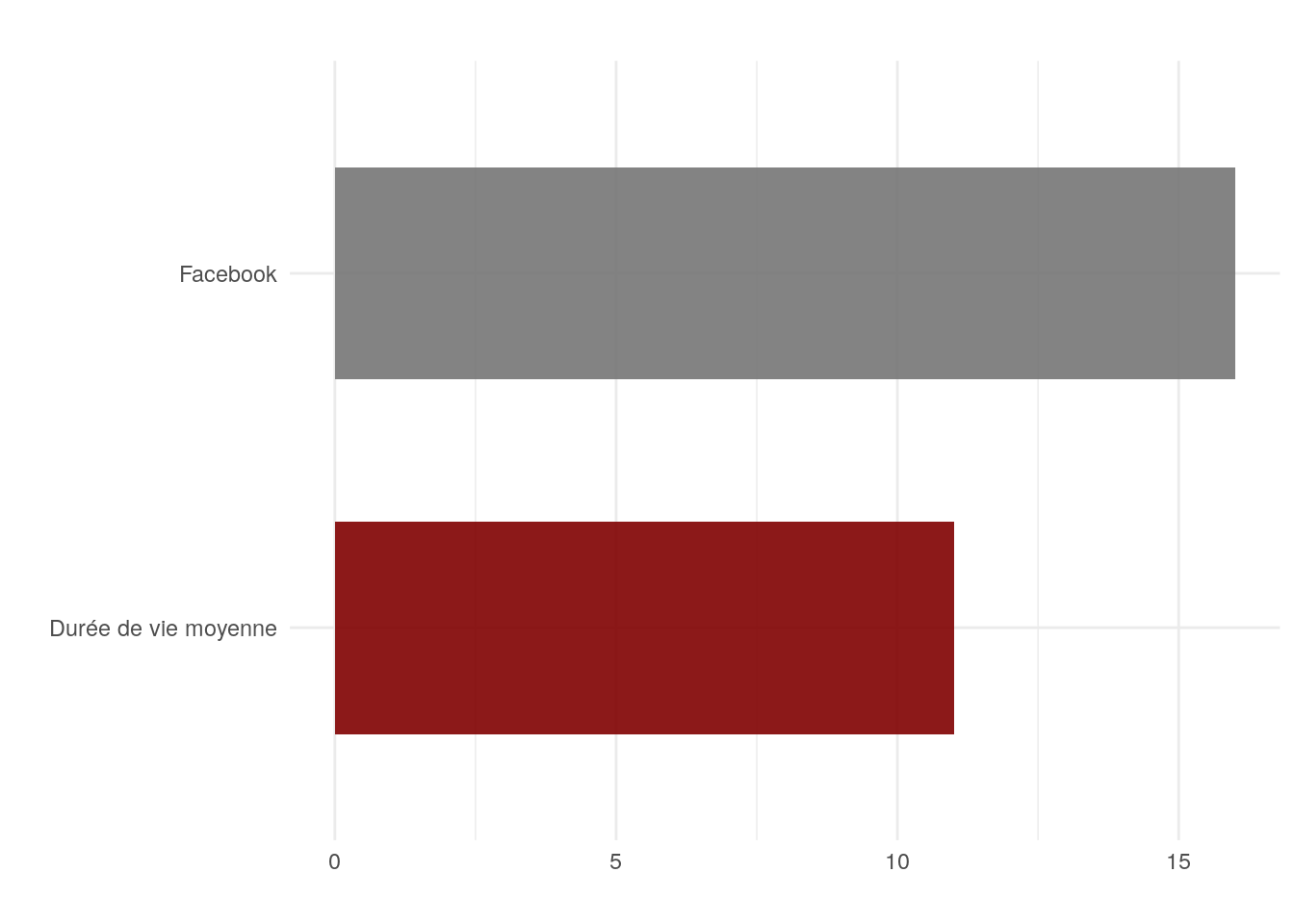
Figure 2.3: Durée de vie moyenne des entreprises d’Internet et exemple de Facebook.

[code]

# Création des données
df <- data.frame(indicator = c("Facebook", "Durée de vie moyenne"),
                 year = c(as.numeric(format(Sys.Date(), "%Y")) - 2004, 11))

# Création du graphique
library(ggplot2)
library(ggsci)
library(ggthemes)
ggplot(data=df, aes(x=year, y=indicator, fill=indicator)) +
  geom_bar(stat="identity", width=0.7, alpha = 0.9) + 
  theme_minimal() +
  xlab("") + 
  ylab("") +
  ggtitle("") +
  theme(legend.position="none") + 
  scale_fill_uchicago()

Productivité moyenne. La productivité moyenne est un indicateur ne concernant qu’un seul facteur de production à la fois. On parlera de productivité moyenne du capital, notée \(PM(K)\), et de productivité moyenne du travail, notée \(PM(L)\). En voici la définition :

La productivité moyenne d’un facteur de production est le volume produit ramené à une unité du facteur de production

\[\begin{equation} \begin{cases} PM(K) = Q/K = f(K,L)/K \\ PM(L)= Q/L = f(K,L)/L \end{cases} \tag{2.3} \end{equation}\]

La figure 2.4 représente la productivité moyenne du facteur travail obtenue à partir de la fonction de production, pour un facteur capital fixe.

On obtient la courbe de productivité moyenne en divisant \(Q\) par \(L\). Par exemple, la productivité moyenne au point \(A\) correspond à la pente de la droite passant par l’origine et par ce point sur la courbe de production. La productivité moyenne atteint donc son maximum pour la droite tangente à la courbe de production, c’est-à-dire au point \(A\).

Figure 2.4: De la fonction de production à la productivité moyenne.

Productivité marginale. Comme la productivité moyenne, la productivité marginale est un indicateur ne concernant qu’un seul facteur de production à la fois. On parlera de productivité marginale du capital, notée \(Pm(K)\), et de productivité marginale du travail, notée \(Pm(L)\). En voici la définition :

La productivité marginale est le volume de production supplémentaire obtenu par l’augmentation d’une unité additionnelle de l’intrant

\[\begin{equation} \begin{cases} Pm(K) = \frac { \partial Q}{\partial K} = \frac{ \partial f(K,L)}{ \partial K} \\ Pm(L)= \frac { \partial Q}{ \partial L} = \frac { \partial f(K,L)}{ \partial L } \end{cases} \tag{2.4} \end{equation}\]

Graphiquement, on obtient la courbe de la productivité marginale en calculant la pente de la tangente de la courbe de la fonction de production en ses différents points (fig. 2.5).

Figure 2.5: De la fonction de production à la productivité marginale.

Si on représente maintenant les courbes de productivité moyenne et de productivité marginale sur un même graphique, on obtient le graphique de la figure 2.6.

Figure 2.6: De la fonction de production à la productivité moyenne et à la productivité marginale.

On obtient les résultats suivants.

• On peut noter que la courbe de la productivité marginale coupe celle de la productivité moyenne en son maximum. Cela provient du fait que la condition pour laquelle la dérivée de la productivité moyenne est nulle (c’est-à-dire le maximum de la courbe de productivité moyenne) est que la productivité moyenne doit être exactement égale à la productivité marginale.
• Du résultat précédent, on tire que la productivité moyenne est croissante lorsque la productivité marginale lui est supérieure et décroissante lorsqu’elle lui est inférieure. En effet, tant que l’usage d’une unité supplémentaire apporte plus que la moyenne des unités déjà employées, cela a pour conséquence d’accroître la moyenne. Lorsque l’unité supplémentaire procure un accroissement de la production inférieur à ce que procurent en moyenne les unités précédentes, la productivité moyenne baisse.
• La productivité marginale est d’abord croissante (jusqu’au point d’inflexion I), puis décroissante. On parle alors de la loi des rendements décroissants.

Loi des rendements décroissants. Voici la définition de la loi des rendements décroissants :

Si l’on accroît la quantité d’un facteur de production tout en maintenant les autres facteurs constants, il existe un point au-delà duquel la production totale va croître à un rythme sans cesse décroissant (courbe convexe, puis concave).Cette loi correspond à une caractéristique habituelle de la plupart des processus de production. Elle est avant tout empirique et permet d’expliquer pourquoi il existe une taille optimale pour une entreprise.

SAP a décidé d’acquérir l’un de ses fournisseurs⁹

Un exemple qui illustre bien la dynamique de marché et l’aspect organique des entreprises et de leurs frontières est la firme SAP. La firme allemande est la firme meneuse sur le marché des progiciels de gestion d’entreprise. Une extension naturelle est la portabilité vers les plateformes mobiles et l’intégration de ces nouveaux outils avec le cœur de métier de l’entreprise. Dans cette logique, plutôt que de développer elle-même des applications sur les nouveaux outils mobiles (tablettes, téléphones intelligents), SAP a décidé d’acquérir l’un de ses fournisseurs et partenaires : Syclo. Syclo est un expert des plateformes mobiles et est venu compléter l’offre de SAP tout en permettant sa migration vers les plateformes mobiles. On peut constater ici que la définition de la taille optimale est aussi une définition que l’on qualifie d’organique, c’est-à-dire dont les contours évoluent avec les innovations technologiques ainsi que la dynamique concurrentielle.

Rendements d’échelle. Envisageons un autre type de modification. Au lieu d’augmenter la quantité d’un intrant en maintenant constante la quantité de l’autre intrant, on augmente la quantité de tous les intrants de la fonction de production. On va donc multiplier par un même facteur constant \(t\) la quantité de tous les intrants \((tK, tL)\) et mesurer l’influence sur la quantité produite, \(f (tK, tL)\). Mathématiquement, cela revient à trouver le degré d’homogénéité \(n\) de la fonction de production (2.5) :

\[\begin{equation} f (tK, tL) =t^n\times f (K, L) \tag{2.5} \end{equation}\]

• Si n= 1, alors les rendements sont constants. L’accroissement de la production est exactement proportionnel à l’accroissement des facteurs (2.6): \[\begin{equation} f (tK, tL) =t^1×f (K, L) \tag{2.6} \end{equation}\]

• Si n> 1, alors les rendements sont dits croissants. L’accroissement de la production est plus que proportionnel à l’accroissement des facteurs (2.7): \[\begin{equation} f (tK, tL) >t ×f (K, L) \tag{2.7} \end{equation}\]

• Si n< 1, alors les rendements sont dits décroissants. L’accroissement de la production est moins que proportionnel à l’accroissement des facteurs (2.8) : \[\begin{equation} f (tK, tL) <t×f (K, L) \tag{2.8} \end{equation}\]

Notion de cycle de vie. Le cycle de vie d’une entreprise peut de façon agrégée être représenté par trois phases successives : les rendements d’échelle croissants caractérisent le développement de l’entreprise, qui passe ensuite par des rendements constants, avant de connaître des rendements décroissants.

La croissance des rendements d’échelle peut être expliquée par la division du travail, la spécialisation des tâches. Et la décroissance peut apparaître pour de très grandes entreprises où il existe très souvent des inefficacités inhérentes. De nombreuses entreprises pratiquent ainsi la filialisation de leurs activités pour éviter de tomber dans cette phase. Aujourd’hui, on parle de plus en plus de la notion de cycle de vie du produit. L’approche de cette discipline est d’étudier toutes les phases de la vie d’un produit depuis sa conception jusqu’à sa disparition du cycle de commercialisation afin d’en tirer des enseignements importants pour la protection de l’environnement.

Progrès technique. Il ne faut pas confondre les effets du progrès technique et les rendements d’échelle. Le progrès technique désigne une déformation de la fonction de production dans le temps : il permet de produire davantage avec les mêmes quantités de facteurs. Par progrès technique, on entend soit une amélioration technologique exogène (RD), soit une amélioration du processus de production au fur et à mesure de la production des volumes (learning by doing, capital humain). La figure 2.7 illustre cette déformation de la fonction de production vers le haut.

Dans le cas des rendements d’échelle, on se déplace sur la courbe de la fonction de production, alors que dans le cas du progrès technique, c’est la courbe qui se déplace (fig. 2.7). Dans ce chapitre, nous ne faisons pas la différence entre progrès technique et innovation. Nous ferons cette différence plus loin lorsque nous traiterons plus longuement de l’innovation.

Toyota : amélioration technologique et amélioration de processus

Toyota est un pionnier en matière et technologie hybrides. Le modèle Prius a fait ses débuts en 1997 - en 2020, Toyota a passé le cap des 15 millions de véhicules hybrides vendus¹⁰ dans le monde. Le fabricant japonais, souhaitant devenir le premier fabricant automobile mondial, a adopté une vision stratégique à long terme mise sur la recherche et l’innovation technologique. Il a parié sur la mise en place de lois environnementales qui viendraient réglementer l’industrie automobile en matière de consommation d’énergie. L’entreprise souhaitait être la mieux placée à ce moment-là dans le domaine des énergies renouvelables et ainsi augmenter ses ventes et sa part de marché. Cette stratégie a porté ses fruits: en 2018, Toyota était le premier fabricant automobile au monde¹¹. Ses ventes de voitures hybrides continuent de monter en flèche, dominant le marché Américain en 2019¹². De plus, Toyota est l’une des seules entreprises bien positionnées¹³ pour faire face aux réglementations environnementales de plus en plus strictes imposées en Europe. Toyota a aussi toujours cherché à améliorer son processus. Le système de production (Toyota Production System)¹⁴ s’efforce de fabriquer des véhicules aussi rapidement et efficacement que possible.

Figure 2.7: Représentation du progrès technique.

La fonction de production est un outil fort pratique lorsqu’il s’agit de schématiser le fonctionnement d’une entreprise. Elle permet de comprendre les liens entre les intrants et les extrants. Certaines industries auront des taux de substituabilité différents entre les intrants et les extrants. Ces derniers iront de parfaitement substituables à complémentaires. La représentation de la fonction de production va aussi évoluer en fonction du progrès technique, des niveaux de production, etc.

L’innovation du secteur bancaire, ou comment rejoindre chaque utilisateur

Tous les dix ans, le secteur bancaire connaît des innovations technologiques modifiant profondément son mode de fonctionnement. Durant les années 1960, les clients effectuaient presque exclusivement leurs transactions dans les succursales bancaires. Avec l’invention dans les années 1970-1980 des cartes à puce, la démocratisation des transactions bancaires s’est progressivement accélérée, notamment à travers la mise en place de guichets automatiques. De cette manière, une banque n’était plus synonyme d’un lieu physique central. La fin des années 1990 et le début des années 2000 correspondent à l’émergence d’Internet et par le fait même ont permis aux particuliers de rentrer sur les marchés boursiers. Depuis 2010, l’émergence du mobile banking, ou des transactions bancaires faites à l’aide de téléphones intelligents, permet au secteur bancaire d’envisager de toutes nouvelles perspectives de croissance : les services M-Pesa de Safaricom en Afrique du Sud ou Google Wallet de Google en sont des exemples. Il est ainsi possible de joindre chaque client en tout temps, et l’accès aux services bancaires n’en est que facilité. Les années 2020 seront probablement caractérisées par une relation plus étroite entre les entreprises technologiques et le secteur bancaire et par l’émergence de nouvelles innovations comme l’IA¹⁵. En effet, ce dernier est déjà employé par 75% de banques avec plus de 100 milliards de dollars d’actifs¹⁶. L’IA peut aider les banques à détecter la fraude¹⁷, interagir avec leurs clients via un chatbot¹⁸, et leur proposer des recommandations personnalisées¹⁹, entres autres innovations. Il est clair que l’influence de l’IA dans le secteur bancaire continuera d’augmenter au cours de la prochaine décennie - la valeur commercial de l’AI est prédit d’atteindre $300 milliards (en dollars américains) d’ici 2030²⁰.

2.3 Modélisation de la technologie

Nous allons représenter différentes combinaisons de facteurs de production pour modéliser la technologie.

2.3.1 Détermination des isoquantes

Pour modéliser la technologie, on utilise une courbe appelée «isoquante» qui relie toutes les combinaisons de facteurs possibles. Cette courbe est différente selon la technologie employée.

Caractéristiques. Pour atteindre le niveau de quantité produite \(Q_0\), on peut mettre en évidence une multitude de combinaisons de facteurs de production \((K_0, L_0)\), \((K_1, L_1)\), etc., que l’on peut représenter par le graphique de la figure 2.8.

Figure 2.8: Combinaisons de facteurs de production pour produire Q_0.

Dans le cas de deux intrants (\(K\) et \(L\)), cette représentation des relations de production s’appelle une isoquante (fig. 2.9), c’est-à-dire l’ensemble de toutes les combinaisons possibles d’intrants \(K\) et \(L\) permettant d’atteindre un niveau donné d’extrants.

Figure 2.9: Isoquante.

Mathématiquement, on doit passer de l’équation de la fonction de production sous la forme \(Q=f (K, L)\) à l’équation d’une isoquante de la forme \(K=g (L)\) pour un niveau de production donné (en effet, on a une isoquante par niveau de production).

Les isoquantes sont le reflet de la technologie à employer dans l’entreprise pour atteindre un objectif de production. Il apparaît évident que l’utilisation de certains facteurs de production est parfois fortement corrélée à l’utilisation préalable d’autres facteurs de production. Par exemple, les facteurs de production employé-machine sont liés : sans employé, les machines ne peuvent pas fonctionner. On parlera alors de facteurs de production complémentaires, mais il existe aussi d’autres cas de figure que nous verrons dans le paragraphe suivant.

Exemples de technologies. Plusieurs cas de figure peuvent être présentés pour définir les facteurs de production utilisés.

Facteurs complémentaires. On dit que les facteurs de production sont complémentaires lorsqu’une quantité donnée d’un facteur ne peut être associée qu’à une quantité déterminée d’un autre facteur (fig. 2.10). Souvent, les intrants sont utilisés en proportions fixes. Par exemple, l’embauche d’un employé entraîne l’achat d’une pelle supplémentaire.

Figure 2.10: Isoquante pour deux facteurs complémentaires.

Dans ce cas, l’optimum, pour un niveau de production donné (\(Q_0\)), est représenté par (2.9) :

\[\begin{equation} f (K, L) = min (K, L) \tag{2.9} \end{equation}\]

Facteurs substituables. On dit que les facteurs de production sont substituables lorsqu’ils sont parfaitement divisibles et adaptables et que le producteur peut remplacer une certaine quantité d’un facteur par une certaine quantité d’un autre facteur à niveau de production égal (fig. 2.11). Par exemple, une banque peut choisir d’installer beaucoup de distributeurs automatiques (DAB), soit d’employer un plus grand nombre de salariés : substitution du capital au travail.

Figure 2.11: Isoquante pour deux facteurs substituables.

Facteurs parfaitement substituables. On dit que des facteurs sont parfaitement substituables si, pour se dispenser d’une unité d’un des deux facteurs, il faut toujours la même quantité additionnelle de l’autre facteur, pour un même niveau de production (fig. 2.12).

Figure 2.12: Isoquante pour deux facteurs parfaitement substituables.

2.4 Facteurs influençant l’impartition et les délocalisations

Certains facteurs peuvent favoriser les délocalisations. À partir de quel seuil une entreprise pense-t-elle à internationaliser sa chaîne de valeur?

2.4.1 Taux marginal de substitution technique

Le taux marginal de substitution technique (TMST) mesure le taux auquel la firme doit remplacer un intrant par un autre tout en maintenant la quantité d’extrant constante. Le TMST du facteur \(K\) au facteur \(L\) est égal à la quantité additionnelle du facteur K qui est nécessaire pour compenser la perte d’une unité du facteur Lafin de maintenir le niveau de production constant.

Supposons que l’on consomme une certaine quantité (\(L_1, K_1\)) et que l’on envisage de réduire la quantité de facteur travail et d’utiliser une quantité additionnelle de facteur capital juste suffisante pour produire la même quantité d’extrant. De quelle quantité supplémentaire \(ΔK\) a-t-on besoin si l’on réduit la quantité de facteur travail de \(ΔL\)? Cette quantité correspond exactement à la pente de la tangenteau point (\(L_1, K_1\)) de l’isoquante (fig. 2.13).

Figure 2.13: Pente de l’isoquante.

Pour déterminer la pente de l’isoquante, on considère une variation des quantités de L et de K telle que l’extrant reste constant (\(ΔQ= 0\)). L’impact sur la production est donné par la différentielle totale de la fonction de production (2.10):

\[\begin{equation} ΔQ=Pm(L)× ΔL+Pm(K)× ΔK= 0 \tag{2.10} \end{equation}\]

En résolvant cette l’expression (2.10), on obtient (2.11) :

\[\begin{equation} TMST_{K,L}= \frac{ΔK}{ΔL}=- \frac{Pm(L)}{Pm(K)} \tag{2.11} \end{equation}\]

Le TMST est donc égal au rapport des productivités marginales des facteurs. Le signe négatif s’explique par le fait qu’il s’agit de diminuer la quantité d’un intrant pour augmenter celle de l’autre. Toutefois, dans le langage courant des économistes, la valeur du TMST est souvent donnée en valeur absolue.

2.4.2 Élasticité de substitution technique

L’élasticité de substitution technique permet de mesurer en pourcentage l’impact, sur les quantités d’intrants, d’une modification des prix relatifs des facteurs. C’est la mesure d’une variation et non pas une mesure absolue. Par conséquent, il faut tenir compte de la combinaison initiale des facteurs de production (\(K/L\)) et du rapport de prix initial (\(P_K/P_L\)) (2.12) :

\[\begin{equation} e_S = \frac{\frac{\delta(K/L)}{K/L}} { \frac{\delta(P_K/P_L)}{P_K/P_L } } = \frac{\delta(K/L)}{\delta(P_K/P_L)} \times \frac{P_K/P_L}{K/L} \tag{2.12} \end{equation}\]

Grâce à ce concept, on peut mesurer l’impact d’une variation sur la structure productive \(K/L\). Une variation de 1 % dans la structure des prix relatifs provoque une variation de eS % de la structure productive (\(K/L\)), et ce, quels que soient les niveaux de départ de \(K\) et de \(L\).

Fonction de production Cobb-Douglas²¹. Il s’agit de la formulation la plus générale des fonctions de production :

\[\begin{equation} Q=A\times K^\alpha\times L^\beta \tag{2.13} \end{equation}\]

où \(A\), \(\alpha\) et \(\beta\) sont des paramètres positifs. Le paramètre A mesure l’échelle de production, c’est-à-dire la quantité d’extrant obtenue pour une unité de chaque intrant. Les paramètres α et β mesurent l’impact sur la quantité d’extrant d’une variation des intrants.

Si l’on s’intéresse à la nature des rendements d’échelle, on constate que :

\[\begin{equation} f(t\times K, t\times L) =A \times (t\times K)^\alpha \times (t\times L)^\beta =t ^{\alpha+\beta} \times f (K, L) \tag{2.14} \end{equation}\]

Ainsi, les rendements d’échelle sont croissants si \(\alpha+\beta> 1\), constantes si \(\alpha+\beta = 1\) et décroissants si \(\alpha+\beta < 1\).

À titre d’illustration, nous allons déterminer le TMST de la fonction Cobb-Douglas. Sachant que le TMST est égal à la fois au rapport des productivités marginales et à la pente de la tangente en un point donné, nous allons procéder à son calcul par les deux méthodes.

1re méthode

\[\begin{equation} TMST = - \frac{Pm(L)}{Pm(K)}= - \frac{A \times \beta \times K^\alpha \times L^{\beta-1}}{A \times \alpha \times K^{\alpha-1} \times L^\beta} = \frac{\beta}{\alpha} \times \frac{K}{L} \tag{2.15} \end{equation}\]

2e méthode

\[\begin{equation} TMST = \lim_{\Delta L \to 0} \frac{\Delta K}{\Delta L} = \frac{dK}{dL}= g'(L) \\ \text{où} \quad K= g(L) = \left( \frac{Q_0}{A \times L^\beta} \right) ^{1/_\alpha} = L^{-\beta/_\alpha} \times \left( \frac{Q_0}{A} \right) ^{1/_\alpha} \\ TMST = \left( - \frac{\beta}{\alpha} \right) \times L^{-\beta/_\alpha-1} \times \left( \frac{Q_0}{A} \right)^{1/_\alpha} = - \frac{\beta}{\alpha} \times \frac{K}{L} \tag{2.16} \end{equation}\]

Le TMST de la fonction Cobb-Douglas est donc décroissant en valeur absolue.

Fonction de production à élasticité de substitution constante (C.E.S.). Cette fonction s’écrit :

\[\begin{equation} f (K, L) = (a\times K^\beta+b×L^\beta)^{1/_\beta} \tag{2.17} \end{equation}\]

où \(a\) et \(b\) sont des paramètres strictement positifs et \(\beta\) est un paramètre positif ou négatif.

2.5 Fonctions de coût de production

Comment représenter les fonctions de coût et ainsi appréhender la dynamique derrière les délocalisations pour raison de coût ?

L’approche de l’économiste est de ramener l’essentiel de sa démarche à une analyse coûts-avantages. En matière d’étude des stratégies d’entreprise, la démarche est la même. L’entreprise va choisir de répondre à la demande en minimisant ses coûts. Cette recherche du coût le plus faible possible permettra de déterminer les quantités d’intrants optimales. Concrètement, connaissant les ventes, l’entreprise passe un certain nombre de commandes auprès de ses fournisseurs.

Remarque. Les coûts de l’économiste ne sont toutefois pas les mêmes que ceux du langage courant. Lecoût d’opportunité représente tout ce à quoi l’on renonce pour faire une action. Il s’agit des coûts directs d’une stratégie, mais aussi des coûts liés au renoncement à une autre stratégie.

Cette section traite de la minimisation des coûts en fonction d’un niveau de production.

2.5.1 Choix optimal des facteurs de production

Optimisation. Parmi l’ensemble des combinaisons de facteurs de production, on va chercher à identifier la combinaison qui minimise le coût de production total pour atteindre le niveau de production d’extrants souhaité.

Droite d’isocoût. La droite d’isocoût (fig. 2.14) représente le budget que s’est fixé l’entreprise pour l’achat des intrants. C’est en quelque sorte le montant des investissements. Connaissant le niveau de production, on cherche à avoir un montant d’investissement le plus faible possible.

Si on dispose de deux facteurs de production, \(K\) et \(L\), dont les prix sont \(P_K\) et \(P_L\), on peut représenter le coût total associé à un niveau de production donné par :

\[\begin{equation} C=P_L×L+P_K×K \tag{2.18} \end{equation}\]

Ainsi, à un niveau de production donné est associé un coût total \(C_0\), que l’on peut représenter par :

\[\begin{equation} C_0=P_L×L+P_K×K \\ \text{d'où} \quad K=\frac{C_0}{P_K} – P_L \times \frac{L}{P_K} \tag{2.19} \end{equation}\]

Cette représentation donne l’ensemble des combinaisons de facteurs respectant ce niveau de coût \(C_0\).

Figure 2.14: Droite d’isocoût.

Minimisation des coûts de production. L’objectif est de minimiser les coûts de production permettant d’atteindre un niveau donné d’extrant \(Q_0\) (fig. 2.15). Cette démarche permettra de déterminer la combinaison optimale des facteurs de production.

Figure 2.15: Recherche du coût minimum

Nous avons vu précédemment la représentation des isoquantes dans le repère \(K=g (L)\). Ces dernières sont le reflet de l’ensemble des combinaisons permettant d’atteindre le niveau de production d’extrants souhaité. Graphiquement, on peut déterminer les facteurs en recherchant le point sur l’isoquante associée à la courbe d’isocoût la plus basse.

Le point correspondant à la minimisation du coût est caractérisé par une condition de tangence. La combinaison optimale en facteurs \(K^*\) et \(L^*\) est obtenue au point C. Les points A et B permettent également de produire \(Q_0\), mais il ne s’agit pas de combinaisons optimales, car elles ne permettent pas de minimiser les coûts.

Pour obtenir analytiquement ce résultat, deux méthodes peuvent être employées: soit on pose l’égalité de la pente de l’isoquante et de la pente de la courbe d’isocoût – ce qui revient à égaliser le TMST au rapport des prix des facteurs –, soit on applique la méthode de Lagrange.

1re méthode

On pose :

\[\begin{equation} TMST =- \frac{P_L}{P_K} \\ \text{d'où } \frac{Pm(L)}{Pm(K)} =- \frac{P_L}{P_K} \tag{2.20} \end{equation}\]

2e méthode

La méthode de Lagrange consiste en un programme de minimisation de la fonction de coût sous la contrainte représentée par l’égalisation de la fonction de production à un niveau donné :

\[\begin{equation} min ~ C=P_K×K+P_L×L \\ \text{sous contrainte} \\ sc\ f (K, L) =Q_0 \\ \text{Ce qui implique} \\ L(K,L,λ)=P_K× K+P_L× L+λ× (Q_0–f(K,L)) \tag{2.21} \end{equation}\]

Les conditions du premier ordre sont :

\[\begin{equation} L′_K= 0 \iff P_K=λ×f ′K \tag{2.22} \end{equation}\]

\[\begin{equation} L′_L= 0 \iff P_L=λ×f ′L \tag{2.23} \end{equation}\]

\[\begin{equation} L′_λ= 0 \iff Y_0=f (K, L) \tag{2.24} \end{equation}\]

Les équations (2.24) et (2.24) amènent :

\[\begin{equation} \frac{P_K} {P_L} = \frac{f′K} {f′L} \tag{2.25} \end{equation}\]

On en tire \(K=g (L, P_K , P_L)\) et, en insérant l’expression dans l’équation (2.25), on obtient \(K^*\) et \(L^*\) en fonction des prix.

Sentier d’expansion. Si le budget du producteur augmente, il peut consacrer davantage de ressources à l’achat des facteurs de production. Dans ce cas, la droite d’isocoût va se déplacer parallèlement à elle-même puisque le cœfficient directeur reste inchangé. À chaque droite d’isocoût correspondra une isoquante et chaque point de tangence fournira l’équilibre du producteur. La courbe qui relie tous ces points d’équilibre est appelée «sentier d’expansion de la firme» (fig. 2.16). Elle exprime l’augmentation des quantités de facteurs utilisés à la suite de l’accroissement des ressources disponibles pour produire.

Figure 2.16: Sentier d’expansion.

Application aux fonctions particulières. Pour la fonction Cobb-Douglas, à l’équilibre, l’élasticité de substitution technique est égale à l’unité. Cela signifie que toute variation de t % dans la structure des prix relatifs provoque une variation de \(t %\) de la structure productive (\(K/L\)), et ce, quels que soient les niveaux de départ de K et de L.

Pour la fonction CES (Constant Elasticity of Substitution), l’élasticité est égale à \(1/(1 +ρ)\).

Pour la fonction à facteurs complémentaires, elle est nulle et infinie pour la fonction à facteurs parfaitement substituables (isoquante linéaire).

Fonction de coût total et ses déclinaisons. Nous avons vu précédemment la représentation du coût total pour un niveau donné de production. Il s’agissait en fait de la somme des différentes quantités des facteurs pondérée par leurs prix.

Toutefois, il y avait autant de «coût total» que de niveaux de production. Il semblerait intéressant de ne disposer que d’une seule fonction de coût total qui donnerait le niveau de coût en fonction des quantités d’extrant Q et non plus d’intrants :

\[\begin{equation} C=C (Q) \tag{2.26} \end{equation}\]

Ainsi, on pourrait appliquer l’ensemble de l’outillage des mathématiques, à savoir étudier par les dérivées les phases croissantes et décroissantes de la fonction de coût. Cette dernière deviendrait un indicateur important pour la gestion optimale de l’entreprise.

Passage de la fonction de coût liée aux facteurs de production à la fonction de coût liée à la quantité produite. Nous savons déterminer par le lagrangien les quantités demandées \(K^*\) et \(L^*\). La demande de ces facteurs de production est fonction de leurs prix et de la quantité d’extrant donnée. Il suffit d’intégrer \(K^*\) et \(L^*\) dans la fonction générale représentant les isocoûts (\(C=P_K×K+P_L×L\)) pour obtenir une fonction de coût dépendant uniquement des quantités d’extrant (fig. 2.17).

Figure 2.17: Fonction de coût total.

Sur le premier graphique de la figure 2.17, pour chaque niveau de production fixé \(Q_1, Q_2\) et \(Q_3\), on obtient les combinaisons optimales des facteurs de production. Ces combinaisons entraînent un coût représenté par les droites d’isocoût.

Ces informations peuvent être représentées sur le second graphique si on pose en abscisse les quantités d’extrant et en ordonnée les différents coûts qui leur sont associés. Ainsi, pour chaque niveau \(Q_1, Q_2\) et \(Q_3\), on peut représenter les coûts associés. Et ceci est reproductible à l’infini, pour obtenir la représentation totale des coûts en fonction des quantités produites.

Caractéristiques de la fonction de coût total. Tous les processus de production entraînent l’utilisation de deux types d’actifs : les investissements fixes et les investissements variables. Les premiers représentent ceux que l’on fait une fois pour toutes sur une certaine période, les seconds sont ceux qui sont directement liés aux quantités d’extrant produites.

On représente la fonction de coût ainsi :

\[\begin{equation} CT=CF+CV \tag{2.27} \end{equation}\]

Cette distinction s’avère également utile pour parler de la différence entre le long terme et le court terme. À court terme, il ne semble pas possible de modifier les investissements fixes. Un entrepreneur ne peut pas décider du jour au lendemain de la délocalisation de son entreprise. Construire un entrepôt représente un coût fixe. Par contre, dans le long terme, tout est possible. La vétusté et l’obsolescence frappent aussi les investissements fixes. Dès lors, il semble tout à fait envisageable, après un laps de temps qui aura permis l’amortissement des investissements fixes, de délocaliser ou de modifier ces investissements. À long terme, tout est variable !

Étude de la fonction de coût total. L’intérêt d’une fonction de coût dépendant des quantités d’extrant est le fait de pouvoir y appliquer les différents outils mathématiques. On étudiera les phases de croissance et de décroissance qui serviront d’indicateurs puissants pour la gestion optimale de l’entreprise.

À partir de la fonction de coût total \(CT(Q) =CV(Q) +CF\), on peut distinguer d’autres concepts : le coût moyen (\(CM\)) et le coût marginal (\(Cm\)).

Coût moyen. La fonction de coût moyen (CM) mesure le coût par unité d’extrant (fig. 2.18). La fonction de coût variable moyen mesure les coûts variables par unité d’extrant (\(CVM\)) et la fonction de coût fixe moyen mesure les coûts fixes par unité d’extrant (\(CFM\)) :

\[\begin{equation} CM(Q) =CFM+CVM \\ CM(Q) = \frac{C(Q)}{Q} = \frac{CV(Q)}{Q}+\frac{CF}{Q} \tag{2.28} \end{equation}\]

Figure 2.18: Courbe du coût moyen.

Les coûts fixes moyens diminuent quand l’extrant augmente, les coûts variables moyens finissent par augmenter quand l’extrant s’accroît et la combinaison de ces deux effets engendre une courbe de coût moyen en U.

Coût marginal. Construite à partir de la fonction de coût total (fig. 2.19), la courbe de coût marginal mesure la variation des coûts engendrés, \(ΔC\), par une variation donnée de l’extrant, \(ΔQ\) (fig. 2.20).

Figure 2.19: Variation des coûts sur la fonction de coût total.

Ainsi, le coût marginal est égal à : \[\begin{equation} Cm(q) = \frac{\delta C(Q)}{\delta Q} \quad \text{et} \quad \lim_{\delta Q \to 0}\frac{\delta C(Q)}{\delta Q} = \frac{dC(Q)}{dQ} \\ \text{d’où } \quad Cm(Q) = \frac{dC(Q)}{dQ} \tag{2.29} \end{equation}\]

Figure 2.20: Courbe de coût marginal.

Relations entre les différentes courbes de coûts. Il est possible de représenter sur un même graphique les différentes courbes de coût. Naturellement, la courbe de coût marginal se déduit de la courbe de coût total, et son minimum correspond au point d’inflexion de la seconde.

La courbe de coût marginal coupe la courbe de coût moyen en son minimum et, lorsque le coût marginal est inférieur au coût moyen, la courbe de coût moyen est décroissante (le supplément de coût engendré par la production d’une unité additionnelle est inférieur à la moyenne du coût des unités déjà produites). Lorsque le coût marginal devient supérieur au coût moyen, la courbe de coût moyen devient croissante. On peut faire la même remarque à propos du coût variable moyen.

Le coût moyen atteint son minimum pour la droite tangente de pente minimum à la courbe de coût total, c’est-à-dire au point B (fig. 2.21).

Le coût variable moyen atteint son minimum pour la droite tangente (ne comprenant pas les coûts fixes) de pente minimum à la courbe de coût total, c’est-à-dire au point A (fig. 2.21).

Figure 2.21: Fonctions de coût.

2.5.2 Relation entre la fonction de coût total et la fonction de production

Les deux égalités suivantes permettent de lier la forme des deux courbes entre elles.Pour le coût moyen variable quand le facteur L est le facteur variable, on a (2.30) :

\[\begin{equation} CVM(Q) = \frac {P_L \times L(Q)}{Q} = P_L \times \frac{L(Q)}{Q} \times \frac{1}{PM(Q)} \tag{2.30} \end{equation}\]

Lorsque le produit moyen augmente (rendements d’échelle croissants), les coûts moyens diminuent : on a besoin de moins d’intrants en moyenne pour produire une unité de bien. Le coût de production est donc plus faible.

Pour le coût marginal du travail (2.31), lorsque le produit marginal augmente, ce sont les coûts marginaux qui diminuent (fig. 2.22) :

\[\begin{equation} Cm(L) = \frac{P_L \times dL(Q)}{dQ} = P_L \times \frac{dL(Q)}{dQ} = P_L \times \frac {1}{Pm(Q)} \tag{2.31} \end{equation}\]

Figure 2.22: Productivité et coûts.

2.5.3 Fonction de coût de longue période et économies d’échelle

On peut tracer les courbes de coût moyen et de coût marginal pour le court terme, mais aussi pour le long terme (fig. 2.23). Les économistes considèrent que la différence entre la courte période et la longue période repose sur la disparition de la notion de coût fixe. En effet, dans le long terme, les coûts fixes sont variables ! Par exemple, une entreprise peut quitter ses locaux pour s’installer dans d’autres. Le hangar, considéré à court terme comme un coût fixe, devient un coût variable à long terme. La période qui coïncide avec le passage de la qualification de coût fixe à celle de coût variable correspond à la période d’obsolescence.

Figure 2.23: Fonction de coût de longue période et économies d’échelle.

Les économies d’échelle correspondent ainsi à la partie décroissante de la courbe de coût moyen de long terme. La partie croissante représente alors des déséconomies d’échelle.

Lorsqu’une entreprise augmente de taille, la baisse du coût moyen qui intervient dans un premier temps s’explique par une plus grande division du travail et par de nombreux facteurs technologiques. Toutefois, une trop grande taille entraîne une augmentation des coûts d’organisation et d’administration.

Par exemple, si on considère les différentes évolutions des coûts de production des diverses phases de production d’une automobile, on voit qu’il existe des montants de production minimale à atteindre pour pouvoir profiter des coûts les plus faibles.

Sur le graphique de la figure 2.24, on peut noter qu’une production minimale de 400 000 unités s’avère nécessaire. S’arrêter à 200 000 unités ne permet pas de tirer pleinement profit des économies d’échelle.

Figure 2.24: Exemples d’économies d’échelle.

Walmart : un contrôle des coûts rigoureux et une stratégie à l’international²²

Le fondateur de Walmart, Sam Wilton, a lancé son entreprise en 1962 en se donnant une règle de base : avoir les prix les plus bas. Il a connu une croissance très rapide dès le début en visant les petites villes où il n’y avait pas d’autres grandes surfaces. Le chiffre d’affaires de Walmart n’a cessé de croître à partir de la première année, où il s’élevait déjà à 975 000 $, pour atteindre en 2019 les 514 milliards²³. L’entreprise a plus de 11 500 magasins²⁴ et 2,2 million d’employés²⁵ à travers le monde.

Pour atteindre ces résultats, Walmart a suivi une stratégie précise reposant sur plusieurs éléments. En plus d’avoir les prix les plus bas, le service et la satisfaction de la clientèle étaient des valeurs essentielles pour Sam Wilton. Le contrôle des coûts était très rigoureux, non seulement les coûts liés aux achats des produits et aux partenariats avec les fournisseurs, mais aussi les coûts du fonctionnement et des opérations. De plus, l’introduction des nouvelles technologies à partir des années 1980 a permis à l’entreprise de se développer sur le plan logistique et d’optimiser les opérations de réapprovisionnement.

En 1991, le premier magasin Walmart hors des États-Unis a ouvert au Mexique. La stratégie d’expansion à l’extérieur des États-Unis s’imposait naturellement après l’expansion connue à l’intérieur du territoire américain. De même, pénétrer le marché chinois, le plus important au regard de la population, devenait essentiel pour que la croissance se poursuive. Toutefois, cela a posé de grandes difficultés, que ce soit en matière de concurrence, de culture locale et d’infrastructures²⁶. Même si la Chine était considérée par les dirigeants de Walmart comme le seul marché où ils pourraient reproduire le même modèle qu’aux États-Unis, la réussite n’était pas pour autant garantie. Malgré les obstacles initials, leurs perspectives commerciales s’améliorent²⁷; ayant noué avec JD.com, un géant chinois du e-commerce, il ont pivoté au secteur épicerie. En 2019, l’entreprise, ayant constaté un taux de croissance chinois élevé, a annoncé un plan d’ouvrir 500 nouveaux magasins.

References

Ritholtz, Barry. 2009. Bailout Nation: How Greed and Easy Money Corrupted Wall Street and Shook the World Economy. John Wiley & Sons.

Ritholtz, Barry. 2012. “Online Empires: Rise & Fall.” The Big Picture. http://www.ritholtz.com/blog/2012/03/online-empires-rise-fall/.

---

9. Adapté de Leena Rao (2012)↩︎

10. https://media.toyota.ca/releases/toyota-passes-15-million-hybrid-electric-vehicles-global-sales↩︎

11. https://www.jato.com/canada/global-car-market-remains-stable-during-2018-as-continuous-demand-for-suvs-offsets-decline-in-sales-of-compact-cars-and-mpvs/↩︎

12. https://www.forbes.com/sites/jimcollins/2020/01/15/toyotas-red-hot-hybrid-sales-prove-that-tesla-is-not-the-only-green-option-for-us-car-buyers/#5b66ef315396↩︎

13. https://electrek.co/2020/02/21/report-at-current-rate-of-ev-deployment-automakers-not-expected-to-meet-eu-co2-targets/↩︎

14. https://global.toyota/en/company/vision-and-philosophy/production-system/↩︎

15. https://www.americanbanker.com/list/the-banking-tech-trends-that-will-dominate-2020↩︎

16. https://www.businessinsider.com/ai-in-banking-report↩︎

17. https://emerj.com/ai-sector-overviews/artificial-intelligence-fraud-banking/↩︎

18. https://www.forbes.com/sites/boblegters/2019/07/15/chatbots-in-banking-got-smart-this-is-how-theyll-make-your-bank-better/#720ea6d770a7↩︎

19. https://newsroom.bmo.com/2019-12-12-BMO-Introduces-AI-Powered-Solution-to-Deliver-Personalized-Banking-Insights↩︎

20. https://www.businessinsider.com/value-of-ai-at-banks-to-reach-300-billion-but-jobs-at-risk-2019-4↩︎

21. Paul Douglas est un économiste du XXe siècle, de l’Université de Chicago, qui fut par la suite sénateur des États-Unis. Charles Cobb est un mathématicien de Amherst College. La fonction Cobb-Douglas a initialement servi à analyser le comportement de la production.↩︎

22. Adapté de Ali Farhoomand (2006)↩︎

23. https://corporate.walmart.com/newsroom/2019/05/16/walmart-releases-q1-fy20-earnings#:~:text=With%20fiscal%20year%202019%20revenue,over%202.2%20million%20associates%20worldwide.↩︎

24. https://corporate.walmart.com/our-story/our-locations↩︎

25. https://corporate.walmart.com/newsroom/company-facts↩︎

26. https://www.businessinsider.com/walmart-in-china-most-popular-international-supermarket-photos-2018-4↩︎

27. https://www.cnn.com/2019/11/21/business/walmart-china-stores/index.html↩︎