Chapitre 13 L’art de la décision stratégique face au risque

Quelle attitude adopter lorsque l’on se trouve placer devant un faisceau d’éventualités ? C’est toute l’affaire de la gestion des risques et de la théorie de la décision : trouver le juste milieu entre la mesure et l’intuition » Peter L. Bernstein (1998)

À retenir

Les économistes ont développé un ensemble d’outils pour comprendre et aider la décision dans l’incertain. Aucun d’entre eux n’est réellement satisfaisant pour l’aide à la décision, par contre, les analyses récentes de la littérature permettent de mieux comprendre les comportements des agents dans l’incertain. Sans pouvoir dire quelle est la meilleure décision stratégique, la meilleure compréhension des actions dans l’incertain permet d’avoir une plus large vision sur l’ensemble des événements possibles. Ce chapitre a également été l’occasion de proposer une relecture et une homogénéisation des concepts de la théorie de la décision avec ceux de la théorie des jeux.

Introduction

La partie I fut l’occasion d’étudier la façon dont les économistes analysent les structures de marché. La partie II mît en lumière les grands types de stratégies à la disposition des entreprises. Mais leur réussite dépend d’une part, des stratégies développées par la concurrence et d’autre part, de l’évolution de la demande. Plus que l’importance des enjeux et des ressources mises en œuvre, c’est l’incertitude qui semble le mieux caractériser les situations stratégiques.

On passe d’une analyse statique à une analyse dynamique. La théorie des jeux devient un allié puissant, notamment avec les hypothèses sur l’information (parfaite / imparfaite et complète / incomplète). Toutefois, la littérature économique avait déjà commencé à réfléchir à la notion d’incertitude liée à la prise en compte de l’aspect dynamique. Cette branche particulière travaille sur un champ appelé « théorie de la décision ». Notre propos dans ce chapitre est de reprendre les enseignements de la théorie de la décision et de les comparer à ceux de la théorie des jeux pour tenter d’en tirer une démarche homogène. Elle servira à mesurer les grands enjeux des choix stratégiques en dynamique : ce que l’on peut appeler « l’art de la stratégie face au risque ».

13.1 Dynamique concurrentielle et information imparfaite

La littérature économique a proposé un ensemble de définitions différentes pour les concepts de risque, d’incertitude et d’information. Nous allons nous appuyer sur les enseignements de la théorie des jeux pour essayer de préciser ces notions.

13.1.1 Dynamique concurrentielle : l’information, source de complexité

Joseph Schumpeter écrivait en 1954 : « Les équilibres multiples ne sont pas nécessairement inutiles, mais dans n’importe quelle science exacte, l’existence d’un équilibre unique est fondamental, même si la détermination de cet équilibre ne s’obtient qu’au prix d’hypothèses très restrictives ; si l’on ne peut prouver l’existence d’un très petit nombre d’équilibres, le champ d’investigation est un chaos qui échappe à toute analyse. »

La dynamique concurrentielle est le fruit de l’ensemble des interactions stratégiques des entreprises. Ces interactions conduisent à des équilibres de court terme. Ils ne sont pas forcément optimaux. De plus, les équilibres peuvent être stables ou instables et même en cas de convergence, l’équilibre de long terme – s’il existe – peut être long à atteindre.

En dehors de l’aspect temporel, la multiplicité des équilibres correspond bien à l’esprit de la dynamique concurrentielle. Le marché connaît des perturbations liées aux interactions stratégiques des entreprises et au degré de rationalité des choix stratégiques réalisés à la période précédente. Ces équilibres se modifient à chaque période en fonction des réactions stratégiques de chaque entreprise à l’équilibre de la période en cours. La dynamique concurrentielle génère ainsi de l’information. Cette information, multiple et changeante, rend la situation complexe. Pour définir une situation complexe, l’approche de Kœnig (1990) est intéressante. Selon lui, la complexité est fonction, d’une part, de la multiplicité des choix stratégiques que peuvent prendre les entreprises et d’autre part, de l’évolution et de la variabilité des interactions entre ces choix. Ainsi, la multiplicité et la variabilité de l’information peuvent être sources d’incertitude. De plus, la rationalité (ou l’irrationalité) des comportements stratégiques ajoute également de l’incertitude.

Mais l’information peut aussi être une réponse. Pour cela, elle doit être de qualité. La difficulté est que son accès sera coûteux. Les agents comparent son coût au gain qu’elle procure, mais aussi au fait que les autres entreprises en aient connaissance. Etre le seul à disposer de certaines informations stratégiques peut donner des avantages concurrentiels, mais peut mener, parfois, à des situations de déséquilibre. En effet, une information partagée peut servir de base commune à l’ensemble des joueurs et jouer le rôle d’un point focal au cours du déroulement d’un jeu stratégique.

13.1.2 Du risque à l’incertitude radicale

H. Simon a souligné que les décisions économiques se prennent toujours en situation d’information imparfaite, parce que l’accès à une information de qualité par rapport à l’ensemble des informations disponibles a un prix. Mais l’information imparfaite n’est pas forcément synonyme d’incertitude. Différents cas de figure peuvent apparaître. C’est à F. Knight (1921) que l’on doit d’avoir opéré pour la première fois une distinction entre la notion de risque et celle d’incertitude. Cette distinction porte sur l’aspect mesurable ou non de la probabilité d’occurrence d’un événement. Toutefois, il n’évoque pas la question concernant l’ensemble des événements possibles : est-il exhaustif ou non ? En d’autres termes, y a-t-il une place à la surprise ou non ?

Le concept de risque correspond donc à un ensemble d’événements dont la probabilité d’occurrence est connue. La logique qui sous-tend cette notion est forcément déterministe : « les probabilités sont « objectives », elles existent par hypothèse au même titre que d’autres grandeurs physiques. Leur valeur est inconnue mais l’expérience permet de s’en faire une idée, selon Loubergé (1994) : «c’est la valeur vers laquelle tend la fréquence d’un événement au fur et à mesure que le nombre d’expériences augmente» . A l’inverse, le concept d’incertitude correspond chez Knight (1921) à un ensemble d’événements dont la probabilité de survenance n’est pas mesurable. Toutefois, l’apparition de la notion de probabilités subjectives – les agents économiques peuvent estimer subjectivement la vraisemblance d’un événement en fonction de leurs informations – a permis de raffiner la définition de Knight. Kreps (1990) tente une homogénéisation des concepts de risque et d’incertitude avec ceux de probabilités subjectives et objectives : selon lui, on parle de risque lorsque les probabilités sont objectives – ce qui correspond à la définition de Knight (1921) – et d’incertitude lorsqu’elles sont subjectives – il s’éloigne alors de Knight (1921). Dans ce dernier cas, la définition de Kreps (1990) est trop restrictive. Kœnig (1990) précise que certains auteurs rajoutent à la définition de l’incertitude de Knight (1921) l’hypothèse de non-exhaustivité de l’ensemble des états de la nature : « par définition, un modèle ignore certains aspects de la réalité»¹³¹ . Il s’agit d’une surprise. L’incertitude correspond alors à une information sur les événements possibles tout en tenant compte que ces événements ne sont pas les seuls, et qu’il peut s’en produire d’autres, inconnus à ce jour. Les événements restant non-probabilisables, la différence de Kœnig (1990) est de considérer un ensemble des événements possibles ouvert. Dans ce cas de figure, Quinn J.B., Mintzberg H. et James R.M. (1988) parlent d’ignorance, notion connue par ailleurs sous le nom d’incertitude radicale : « Dans le cas d’un processus nouveau comme celui du verre flotté, il n’importe pas tant de garder secret le détail du procédé, que de laisser les concurrents dans l’ignorance de la possibilité même d’un tel procédé. »¹³²

Figure 13.1: Proposition d’une classification des situations entre le contexte de risque et celui d’incertitude radicale.

13.1.3 Théorie des jeux et information imparfaite : une relecture des concepts

La conciliation entre les définitions précédentes et les concepts de la théorie des jeux est possible. Dans l’axiomatique de la théorie des jeux, l’information peut prendre deux assertions : parfaite / imparfaite et complète / incomplète.

L’information parfaite (imparfaite) correspond à une situation où le joueur (ne) connaît (pas) sa position dans l’arbre du jeu, en d’autres termes, il (ne) sait (pas) ce que l’autre joueur a joué avant lui dans un jeu séquentiel.
L’information complète signifie que l’ensemble des stratégies, des événements et des paiements sont connus.

Des rapprochements existent donc entre ces notions et celles de la «théorie de la décision».

La notion de risque – ensemble fermé des événements avec probabilités objectives – correspond à l’hypothèse d’information complète en stratégies mixtes.
La notion d’incertitude – ensemble des événements ouvert non-probabilisable – correspond à l’hypothèse d’information incomplète en stratégies pures (ou mixtes si probabilités subjectives).

Si l’on considère un ensemble d’événements non exhaustif (et donc ouvert), on peut distinguer la notion d’incertitude et celle l’incertitude radicale. Ainsi, l’incertain correspond, à l’existence d’événements non-anticipés ou de gravité non anticipée, mais connus par ailleurs.

Exemple Toute entreprise qui s’était installée à Kobé au Japon avait connaissance des risques sismiques. Et même en tenant compte des règles de précaution en matière de construction, le pire n’a pu être évité, le 15 janvier 1995, dans la mesure où le tremblement de terre a atteint une violence inhabituelle non anticipée.

L’incertitude radicale correspond à la possibilité d’occurrence d’événements non-anticipés car ne pouvant pas être identifiées en l’état de la connaissance scientifique du moment. C’est, par exemple, une entreprise qui n’a pas tenu compte dans ses décisions stratégiques de l’introduction sur le marché d’un procédé technologique innovant par une entreprise concurrente.

Exemple

Une entreprise pharmaceutique lance un nouveau vaccin sur le marché. Des études poussées lui ont permis d’estimer l’ensemble des effets secondaires et les probabilités de survenance de ces effets. Toutefois, lors de la diffusion du vaccin et en raison de la complexité de l’organisme humain, des effets secondaires non-anticipables peuvent apparaître. L’entreprise pharmaceutique passe d’une situation qu’elle croyait risquée à une situation d’incertitude radicale. La réalisation d’un tel basculement va entraîner des coûts (liés au retrait de vaccin du marché, au dédommagement des victimes,…). Pour se protéger, les entreprises doit apporter la preuve de la non connaissance scientifique de tels effets au moment du lancement du vaccin et se préparer à gérer une telle crise (cf. encadré 1)

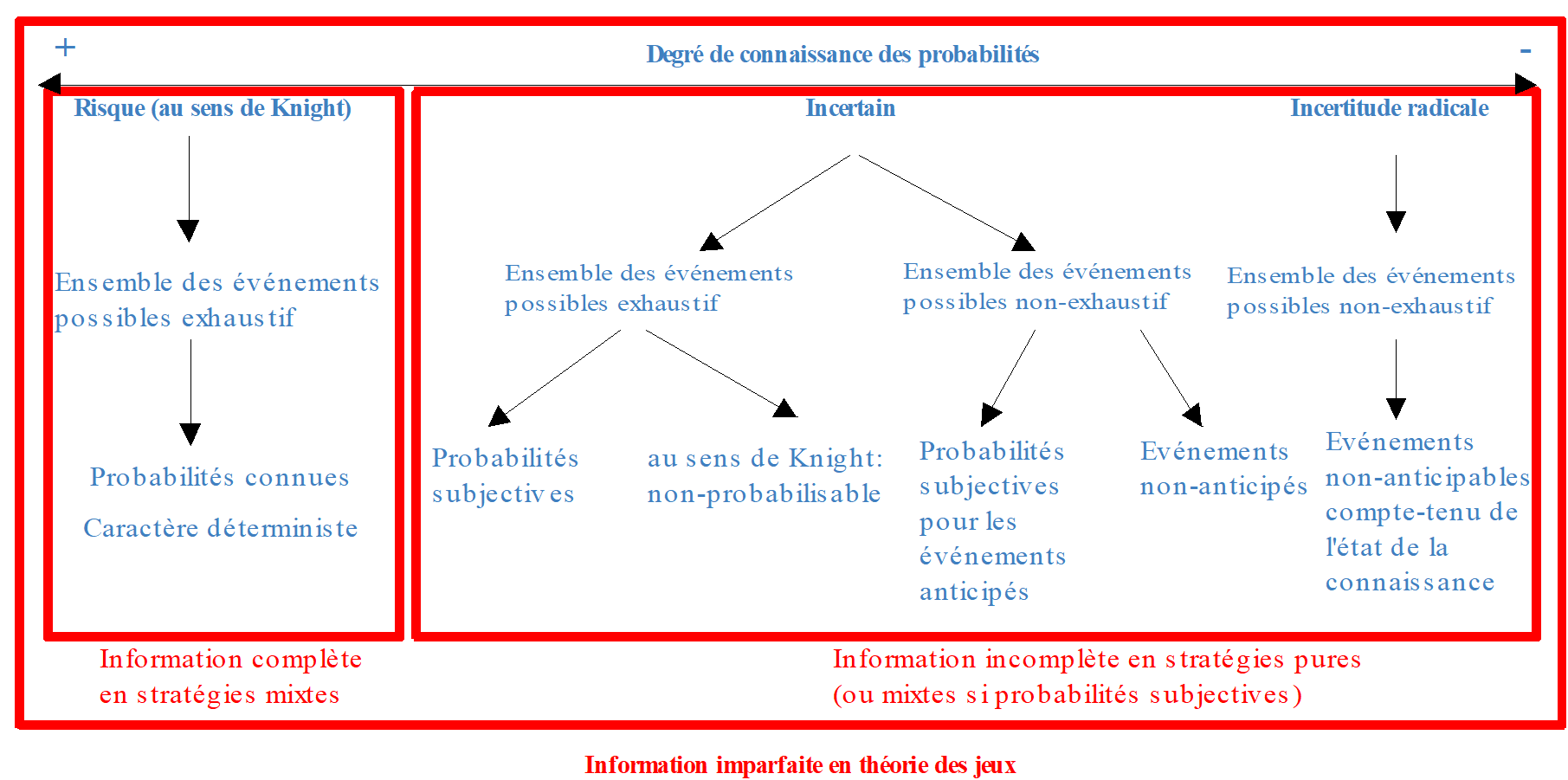
Figure 13.2: Théorie des jeux et théorie de la décision: des liens possibles.

Encadré 1 : Le téléphone portable est-il dangereux pour la santé ? Source : Plan de communication de Bouygues Telecom, juin 2000

Dans la production et la commercialisation des téléphones portables, tous les risk-managers auraient défini la situation comme étant risquée plutôt qu’incertaine, au sens de Knight. Les événements possibles sont connus et des probabilités peuvent leur être associées. Pourtant une question est apparue : « est-ce que les radiofréquences émises par le téléphone portable ne sont pas dangereuses pour la santé ? ». Les études menées en Europe, aux Etats-Unis concluent par la négative. Mais ces résultats ne sont « vrais » que dans l’état actuel de la connaissance scientifique. Peut-être s’apercevra-t-on dans quelques années que le téléphone portable est véritablement nocif. Pour exemple, l’amiante était « considérée inoffensive » dans les années 70. Pour éviter d’être tenu responsable si l’ensemble des événements envisagés n’est véritablement pas exhaustif, Bouygues Telecom a décidé de mener une campagne de communication qui annonce aux utilisateurs que, pour l’instant, aucune connaissance sur le sujet ne permet de valider ou d’invalider ces hypothèses. L’entreprise de téléphonie utilise le « principe de précaution»¹³³ .

Cette tentative de clarification des concepts et d’homogénéisation entre ces deux littératures, que sont la théorie de la décision et la théorie des jeux, semble importante à partir du moment où cette dernière s’impose comme l’outil moderne d’analyse de l’incertitude.

Pour développer une stratégie, l’entreprise doit donc répondre à plusieurs questions : 1. L’ensemble des événements possibles est-il exhaustif ou non ? (même si on croît qu’il l’est, toujours se préparer au cas où un événement non anticipable apparaîtrait). 2. Peut-on associer des probabilités (objectives ou subjectives) à chaque événement ? 3. Quels sont les résultats associés à la réalisation de chaque événement ? 4. L’autre joueur dispose-t-il de la même information ? 5. Quelles sont les stratégies offertes à l’autre joueur ?

L’exemple suivant va servir d’appui pour l’étude des critères de décision dans le risque mais aussi dans l’incertain (section 3). Pour lancer un nouveau produit hautement technologique, une entreprise a le choix entre trois modes de production : soit elle choisit de former un consortium avec quelques uns de ses concurrents (C), soit elle décide d’intégrer l’un de ses concurrents afin de bénéficier d’économies d’échelle (I) ou soit elle choisit d’investir seule dans la recherche et le développement (S). La concurrence sur le marché du produit que l’entreprise veut lancer peut être soit forte (1), soit moyenne (2) ou soit faible (3). Les résultats dépendront de l’état de la nature qui se réalisera, c’est à dire du niveau de concurrence avéré (1), (2) ou (3) et du moyen choisi (C), (I) ou (S).

	(1)	(2)	(3)
Consortium (C) :	10	20	30
Intégration (I) :	4	25	30
Solitaire (S) :	5	15	50

Nous allons étudier les différents choix possibles et définir la stratégie la mieux adaptée à l’environnement. Nous allons présenter les différents critères de décision qui vont permettre de choisir une stratégie en situation de risque (section 2) et d’incertitude (section 3). Un critère est une fonction qui associe un nombre à chaque décision et qui croît avec les préférences du décideur.

13.2 Choix stratégiques en environnement risqué

Dans un environnement risqué au sens de Knight (1921), les probabilités d’occurrence des événements sont connues, et nous avons vu qu’elles ont été nommées, plus tard, « objectives ». Lorsque l’on connaît une distribution de probabilité, il semble aisé d’en déduire des critères de décision. Dans les sciences sociales, pourtant, des précautions et des raffinements doivent être étudiées si l’on ne veut pas arriver à des conclusions éloignées de toute réalité. Un premier exemple est celui concernant le critère de décision basée sur l’espérance mathématique des résultats.

13.2.1 Les limites du critère de l’espérance mathématique : le paradoxe de Saint-Pétersbourg

Nous allons nous intéresser aux situations où les probabilités des états sont connues ou du moins appréciées numériquement (on note pi la probabilité d’occurrence de l’état i). C’est au XVII^e siècle que Pascal¹³⁴ à la demande d’un joueur de cartes passionné, le chevalier de Méré, a découvert les bases du calcul des probabilités. Le critère de l’espérance mathématique est le plus ancien des critères utilisés pour évaluer une situation risquée, qu’il s’agisse de gains ou de pertes. En 1657, le Hollandais Christian Huygens rédige la première table de mortalité. Ce dernier donna la définition suivante de l’espérance mathématique : « c’est le juste prix auquel un individu accepterait de céder sa place dans une partie. »

Reprenons notre exemple sur la production d’un produit hautement technologique et considérons que les trois états de concurrence ${e1, e2 et e3}$ sont affectés des probabilités $½$, $¼$ et $¼$. Les choix de l’entrepreneur prennent la forme de « loteries » : par exemple, s’il choisit C, il a une probabilité $½$ de gagner 10, une probabilité $¼$ de gagner 20 et une probabilité $¼$ de gagner 30. Nous allons étudier les comportements de choix des individus dans un tel contexte.

13.2.1.1 Le critère de l’espérance mathématique

Le décideur va pondérer le résultat associé à la réalisation de l’état de la nature par la probabilité qui lui est associée. Pour chaque stratégie, il calcule l’espérance mathématique des résultats :

\[\begin{equation} E(d)=\sum_{i=1}^{n} p_i\times c_i(d) \tag{13.1} \end{equation}\]

La solution optimale correspond à la stratégie qui à plus forte espérance.

$E(C) = ½ (10) + ¼ (20) + ¼ (30) = 70/4$, $E(I) = 63/4$ et $E(S) =75/4$. Le critère de l’espérance mathématique rangerait les décisions dans l’ordre S, C, I.

Mais ce critère n’est pas satisfaisant. Moins d’un siècle après Huygens, des paradoxes liés à la nature même de l’être humain sont apparus. Le plus célèbre d’entre eux est celui du mendiant de Saint-Pétersbourg mis en évidence par Nicolas Bernouilli au début du XVIII^(ème) siècle.

13.2.2 Le paradoxe de Saint Pétersbourg et le critère de Bernoulli

Exemple

« Un mendiant de la ville de Saint-Pétersbourg détenait un billet de loterie pouvant lui faire gagner 20 000 ducats avec une probabilité égale à 0.5. Un riche marchand lui propose de lui racheter son billet 9000 ducats. Le mendiant accepte l’échange. Selon le critère de l’espérance de gain, il aurait du refuser car ce ticket valait 10 000 ducats. »

Mise en évidence du paradoxe

Ce paradoxe peut être modélisé. Daniel Bernouilli (1738), cousin de Nicolas, a proposé le jeu suivant. Considérons un jeu de pile ou face. On lance une pièce en l’air jusqu’à ce que face apparaisse. Si face apparaît pour la première fois au n-ième jet, vous gagnez 2n dollars. Dès que face apparaît, le gain est empoché et le jeu s’arrête. Combien seriez-vous prêt à payer pour participer à ce jeu ? Toute votre fortune ?

Nous allons utiliser le critère de l’espérance de gain pour évaluer un tel jeu :

\[\begin{equation} E(G) = ½ \times 2 + (½)^2 \times 2 + (½)^3 \times 3 +...+(½)^n \times 2^n = 1+1+...+1 = + \infty \tag{13.2} \end{equation}\]

L’espérance de gain de ce jeu est infinie. Cela veut dire qu’il est possible que quelqu’un décide de parier une somme très élevée – voire infinie – pour tenter de gagner à ce jeu une somme infinie. Or, personne ne risquerait toute sa fortune dans un jeu même si l’espérance de gain est infiniment grande. Selon Daniel Bernouilli (1738), une telle perspective de gain aurait du susciter l’intérêt de nombreux joueurs et provoquer des mises importantes.

Exemple Le jeu de Saint-Pétersbourg est transposable aux organisations industrielles. Il existe des marchés à fort potentiel sur lesquels les espérances de gain sont très élevées, mais dont la probabilité de réalisation est très faible en raison de la concurrence. Une façon d’augmenter cette probabilité est de faire de lourds investissements de recherche et développement, et/ou de procéder à des intégrations verticales afin d’éliminer la concurrence et d’augmenter ses chances, etc. Pourtant, même avec une espérance de gain infinie, aucune entreprise n’est prête à investir une somme presque infinie.

L’hypothèse suggérée par le suisse Cramer (1728) à son compatriote Daniel Bernoulli (1738)¹³⁵ pour résoudre ce paradoxe est que, si chaque personne n’est prête à miser qu’une somme finie, disons 100 dollars, pour jouer à ce jeu, c’est que cette somme ne correspond pas au gain espéré mais à l’espérance d’une fonction de gain. C’est cette fonction qui traduit une certaine forme d’aversion au risque (risque de perdre toute sa fortune pour ne gagner que 2 dollars), et qui croit de moins en moins vite avec le gain. Cette fonction U est appelée utilité du gain et 100 est donc le prix que l’on est prêt à payer pour jouer à ce jeu. $EU(G) < + $:

\[\begin{equation} EU(G) = ½ \times U(2) + (½)^2 \times U(2^2) + (½)^3 \times U(2^3) +...+(½)^n \times U(^2n) = 100 \tag{13.3} \end{equation}\]

On peut chercher à déterminer la fonction d’utilité $U$ qui justifie que l’individu, par exemple, ne misera pas plus de 100 dollars pour jouer à ce jeu. On voit bien que selon le choix de la fonction le montant sera différent. Si le mendiant a accepté l’échange, c’est que ce n’était pas le gain lui même qui lui importait mais plutôt l’utilité que ce gain lui procurait.

Critère de Bernoulli

Pour chaque stratégie, on va évaluer l’espérance des utilités des résultats pondérés par les probabilités de survenance:

\[\begin{equation} EU(d)=\sum_{i=1}^{n} p_i\times U[c_i(d)] \tag{13.4} \end{equation}\]

Nous allons classer les stratégies par espérance d’utilité croissante. Avant cela il faut définir la forme de la fonction U. D’après Daniel Bernoulli, la satisfaction des individus augmente toujours avec la richesse (fonction U croissante) mais de moins en moins vite au fur et à mesure qu’ils s’enrichissent (principe de l’utilité marginale décroissante). Les fonctions d’utilité qui vérifient ces deux hypothèses doivent donc être croissantes et concaves. Considérons par exemple le cas d’une fonction d’utilité logarithmique. On peut reprendre notre exemple de choix de stratégie de production : $EU(C) = ½ U(10) + ¼ U(20) + ¼ U(30) = 2.75$, $EU(I) = 2.35$ et $EU(S) = 2.46$. Si le comportement du décideur correspond au principe énoncé, le critère de l’utilité espérée range les décisions dans l’ordre : C, S, I.

Pendant deux siècles, la solution de D. Bernouilli a perduré, essuyant quelques revers. La critique la plus forte est celle de Marshall selon qui les individus choisissant sur la base de l’espérance d’utilité et ayant une utilité marginale décroissante ne prennent jamais de risque. La pratique du jeu échappe donc totalement à la formulation bernouillienne. La théorie de l’utilité espérée sera réhabilitée grâce aux travaux de von Neumann et Morgenstern en 1944. La loi de l’utilité marginale décroissante est alors abandonnée comme principe explicatif général des choix individuels. L’espérance d’utilité est en revanche préservée pour les représenter.

[Code en R]

payoffs<-c()
for (i in 1:1000) {
  k<-1
  while (sample(c("H","T"),1)!="H") {
    k=k+1
  }
  payoffs<-c(payoffs, 2**k)
}
summary(payoffs)

13.2.3 L’utilité espérée et ses apports

Le critère de l’utilité espérée a été généralisé et construit de manière théorique par Von Neumann et Morgenstern (1944) . Cette théorie a été développée dans le cadre de situation de risque. Le principe fondamental est qu’en situation de risque, le comportement du décideur est entièrement déterminé par ses préférences sur les distributions de probabilité des conséquences de ses actions.

13.2.3.1 L’axiomatique

La théorie de von Neumann et Morgenstern a pour objet des comparaisons de loteries (cf les loteries de notre exemple de choix de production). Un décideur doit pouvoir définir un ordre de préférence complet dans l’ensemble des situations possibles¹³⁶. $U(L)$, appelée utilité du décideur pour la situation L, doit permettre d’associer un nombre à toute situation $L$ tel que :

\[\begin{equation} \begin{cases} U(L) > U(L’) ~\text{si et seulement si L est préféré à}~L’ \\ U(L ) = U(L’) ~\text{si et seulement si les deux situations sont équivalentes.} \end{cases} \tag{13.5} \end{equation}\]

Pour définir la rationalité du décideur, von Neumann et Morgenstern ont défini une relation de préférence $\succ$ sur l’ensemble des loteries $L$ (considéré comme l’ensemble de toutes les distributions de probabilité des richesses finales possibles) qui vérifie les axiomes suivants :

Axiome 1 : (Axiome de comparabilité) Le décideur est capable de préordonner complètement les loteries L dans l’ensemble des loteries sur les conséquences :

\[\begin{equation} \forall L', L'' \in L\text{, soit } L'\succ L'' \text{, soit } L''\succ L'\text{, soit } L'\sim L'' \tag{13.6} \end{equation}\]

Axiome 2 : (Axiome de transitivité) Il y a une certaine cohérence dans les classements :

\[\begin{equation} \forall L', L'', L''' \in L\text{, soit } L'\succ L'' \text{et } L''\succ L'''\text{alors } L'\succ L''' \tag{13.7} \end{equation}\]

Axiome 3 : (Axiome d’indépendance) Une combinaison convexe de distributions ne doit pas modifier les préférences :

\[\begin{equation} \forall L', L'', L''' \in L, ~\forall \alpha \in [0,1]~\text{on a :} // L'\succ L'' \iff \alpha L'+(1-\alpha)L'''\succ \alpha L''+(1-\alpha)L''' \tag{13.8} \end{equation}\]

Axiome 4 : (Axiome de continuité) Une distribution comprise entre deux autres pourra toujours être dominée par une combinaison linéaire des deux autres et pourra toujours dominer une autre combinaison linéaire des deux autres distributions :

\[\begin{equation} \forall L', L'', L''' \in L, ~\forall \alpha, \beta \in [0,1]~\text{on a :} // \text{Si } L'\succ L''\succ L''' \text{ alors } \alpha L'+(1-\alpha)L'''\succ L''\succ \beta L'+(1-\beta)L''' \tag{13.9} \end{equation}\]

Théorème de von Neumann et Morgenstern : Si la relation de préférence $\succ$ sur un ensemble $L$ vérifie les axiomes A1, A2, A3 et A4, alors il existe une fonction d’utilité $U:\Re \to \Re$ continue, strictement croissante et unique à une transformation affine croissante près telle que :

\[\begin{equation} \forall L', L'' \in L ~ L' \succ L'' \iff U(L')>U(L'') // \text{avec } U(L)=\sum_{i=1}^{n}p_iU(c_i(d_i)) \tag{13.10} \end{equation}\]

La fonction U(L) est linéaire par rapport aux probabilités.

Le choix de la fonction d’utilité est assez large. Toutefois, cette fonction d’utilité doit être conforme au comportement de l’individu et refléter son attitude face au risque.

13.2.3.2 Représentation des préférences et attitude par rapport au risque

Considérons un individu possédant une richesse initiale $W$ et détenant une loterie $\tilde{x}$ , ( $\tilde{x}$ étant une variable aléatoire). Sa richesse finale est égale à $W+\tilde{x}$. L’individu a le choix entre conserver la loterie (sa richesse finale est donc aléatoire) ou obtenir $E(W+\tilde{x})$ avec certitude. S’il préfère $E(W+\tilde{x})$, c’est à dire une somme certaine, on dira qu’il est averse au risque. S’il choisit de conserver la loterie, on dira qu’il aime le risque.

Notion d’équivalent certain

Lorsqu’il faut choisir entre un résultat incertain et un résultat certain, non aléatoire, l’équivalent certain désigne la quantité de revenu certain qui rendra le choix indifférent. Ce sera, par exemple, le prix maximal qu’un joueur sera prêt à payer pour un billet de loterie : le joueur est indifférent entre le billet de loterie et la somme de monnaie correspondante à son prix. La valeur investie dans un actif risqué est l’équivalent certain des rendements possibles de cet investissement.

Si l’on calcule l’utilité espérée d’un titre financier T qui peut rapporter 1000 dollars avec une probabilité $\frac{1}{4}$ ou 100 dollars avec une probabilité $\frac{3}{4}$ on aura dans le cas d’une fonction d’utilité logarithmique :

\[\begin{equation} EU(T) = \frac{1}{4} U(1000) + \frac{3}{4} U(100) = 5,18 \tag{13.11} \end{equation}\]

L’équivalent certain du titre financier est donc tel que $U(EC) = EU(T) = 5,18$ d’où $EC = e^{5,18} = 178$. Pour un investisseur détenir ce titre est équivalent à détenir 178 dollars.

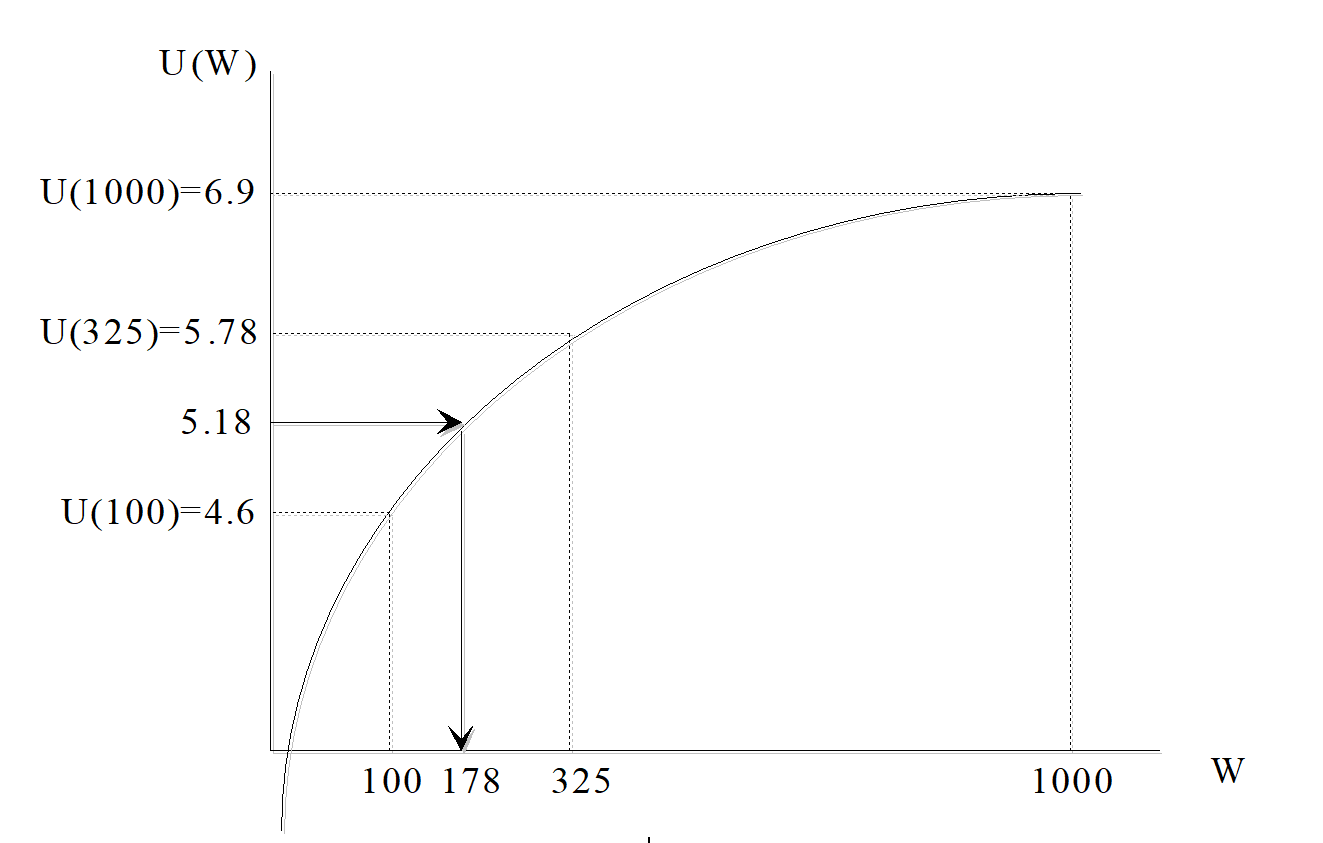
Figure 13.3: Fonction d’utilité et équivalent certain.

Cette notion d’équivalent certain permet de comparer différentes situations de risque. De plus, en observant les équivalents certains d’un agent, il devient possible de caractériser sa fonction d’utilité.

Comportements face au risque

Soit la loterie $ = L ( h, -h ; ½, ½)$, qui correspond à deux possibilités : soit gagner $h$ avec une probabilité $½$, soit perdre $h$ avec la même probabilité $½$. La richesse finale est donc $W+\tilde{x}$ c’est à dire, $W+h$ avec une probabilité $½$ et $W-h$ avec une probabilité $½$. L’individu est supposé avoir le choix entre la loterie $\tilde{x}$ (et donc un gain final aléatoire) et le gain moyen $E(W+\tilde{x})$, certain. Sous certaines conditions, il va soit préférer le gain certain, soit être indifférent entre les deux propositions, ou soit préférer la loterie. On a :

\[\begin{equation} \begin{cases} E(G) = E(W+\tilde{x}) = ½ (W+h) + ½ (W-h) = W \\ U(E(G)) = U(E(W+\tilde{x})) = U(W) \\ E(U(G)) = E(U(W+\tilde{x})) = ½ U(W-h) + ½ U(W+h) \end{cases} \tag{13.12} \end{equation}\]

Aversion au risque : L’individu qui va préférer la somme certaine sera réputé risquophobe. Ainsi, en termes d’utilité :

\[\begin{equation} u(E(G))>E(u(G))\\ \text{donc } E(W+\tilde{x})\text{ sera préféré à } (W+\tilde{x}) \text{ si et seulement si } u(E(W+\tilde{x}))>E(u(W+\tilde{x}))\\ \rightarrow U(W)>1/2 U(W-h)+1/2 U(W+h) \end{equation}\]

Pour un agent averse au risque, l’équivalent certain ($EC$) de la loterie est inférieur à son gain moyen ($W$). L’agent préfère une situation inférieure mais certaine à une situation où il risque de perdre. La fonction d’utilité est concave dans un graphique où la richesse est mesurée par l’axe horizontal, et l’utilité de la richesse par l’axe vertical. Cela représente la décroissance de l’utilité marginale. C’est l’esprit de l’essai publié par Daniel Bernouilli (1738) qui parlait de la peur du risque.

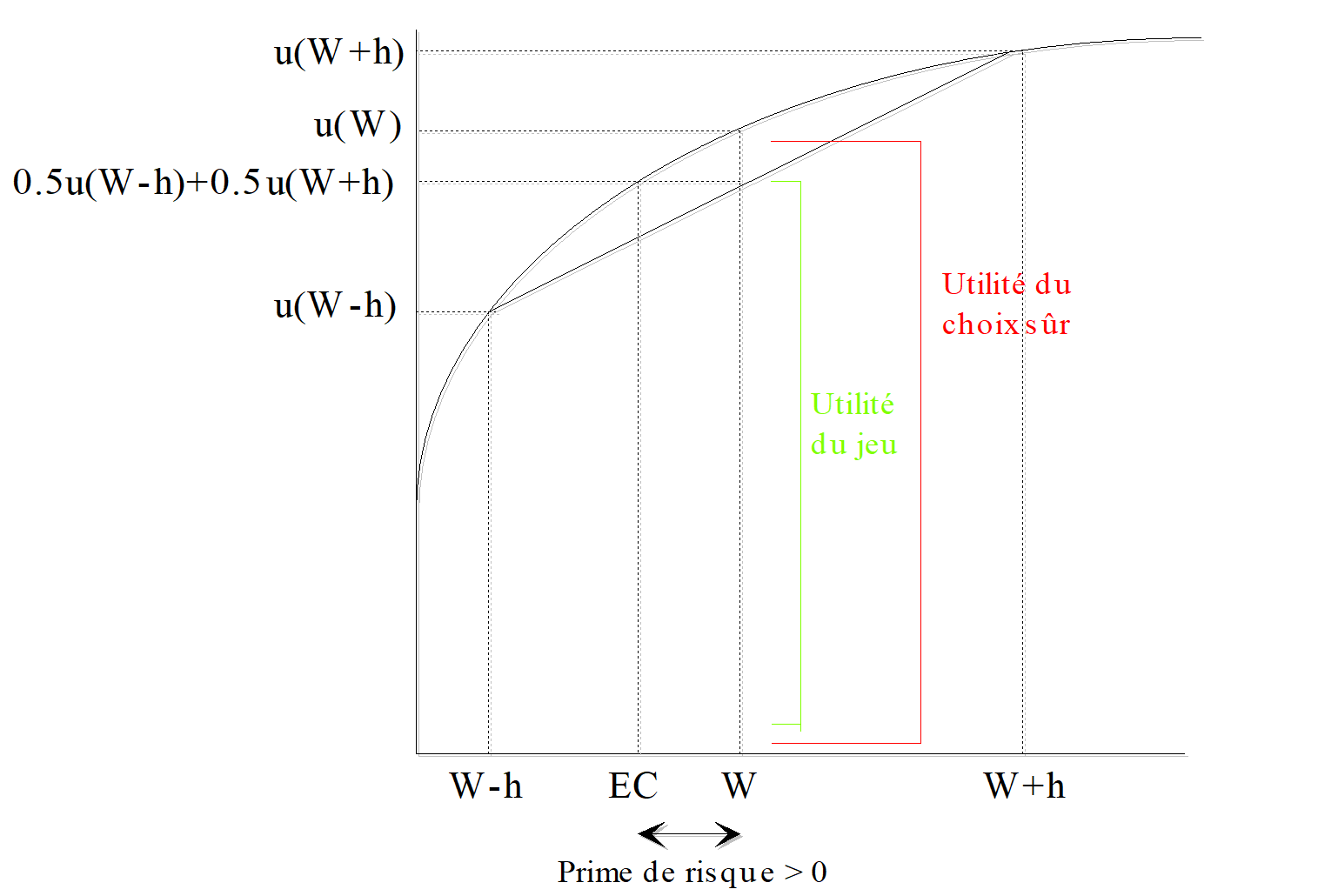
Figure 13.4: Représentation de la fonction d’utilité d’un individu averse au risque.

On peut définir la notion de prime de risque associée à une loterie comme le montant qu’un individu est prêt à payer pour ne pas avoir à encourir le risque. Si l’on reprend la définition de l’équivalent certain, qui est égal à la différence entre le gain moyen et la prime de risque, on en déduit : $\Pi = E(G) – EC$

Neutralité au risque : Un agent est neutre au risque lorsqu’il est indifférent entre une loterie et le gain moyen que lui procure cette loterie. Soit :

\[\begin{equation} u(E(G)) = E(u(G)) \\ E(W+\tilde{x}) ~\text{sera équivalent à } (W+\tilde{x}) ~\text{si et seulement si } u(E(W+\tilde{x}) )= E(u(W+\tilde{x})) \\ \implies U(W) = \frac{1}{2} \times U(W-h) + \frac{1}{2} \times U(W+h) \end{equation}\]

La fonction d’utilité est linéaire : sa représentation est une droite. La prime de risque est nulle : l’équivalent certain est égal au gain moyen. L’utilité marginale de l’agent est constante : à chaque fois qu’il reçoit un euro de plus, son utilité augmente de la même quantité.

Cet agent est neutre au risque, pourtant un événement certain est moins risqué qu’une loterie. Or, dans ce cas, il « oubliera » de telles incertitudes et ne considérera que l’espérance de gain de chacune de deux loteries.

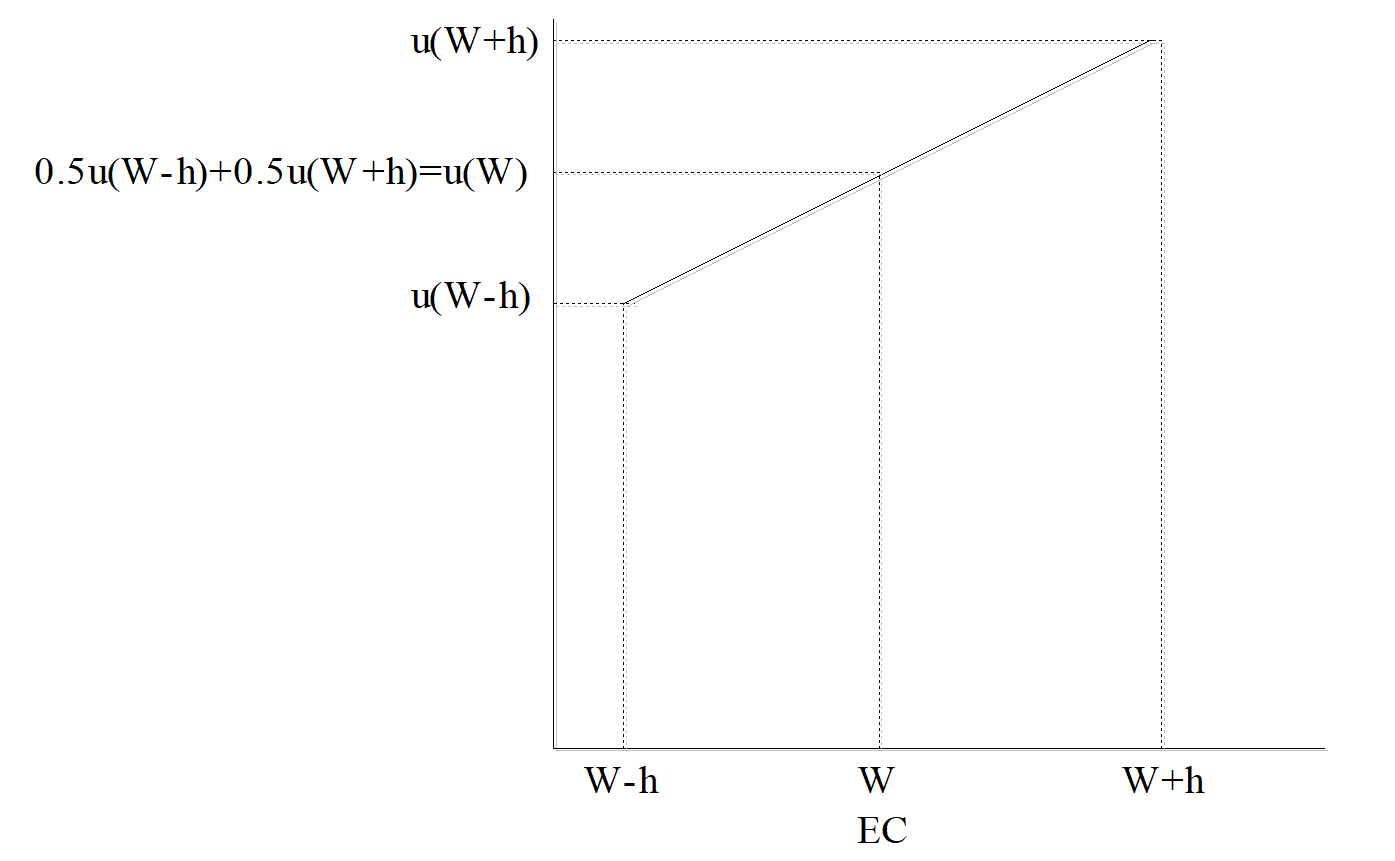
Figure 13.5: Représentation de la fonction d’utilité d’un individu neutre au risque.

Propension pour le risque :

Un agent qui aime le risque sera prêt à accepter une somme d’argent pour ne pas participer à la loterie. Dans ce cas, la prime de risque sera négative. L’équivalent certain sera supérieur au gain moyen.

\[\begin{equation} u(E(G)) < E(u(G)) (W+\tilde{x}) ~\text{sera préféré à } E(W+\tilde{x}) ~\text{si et seulement si } u(E(W+\tilde{x})) < E(u(W+\tilde{x})) \\ \implies U(W) <\frac{1}{2} U(W-h) + \frac{1}{2} U(W+h) \end{equation}\]

La fonction d’utilité est convexe, représentant un agent ayant une utilité marginale croissante.

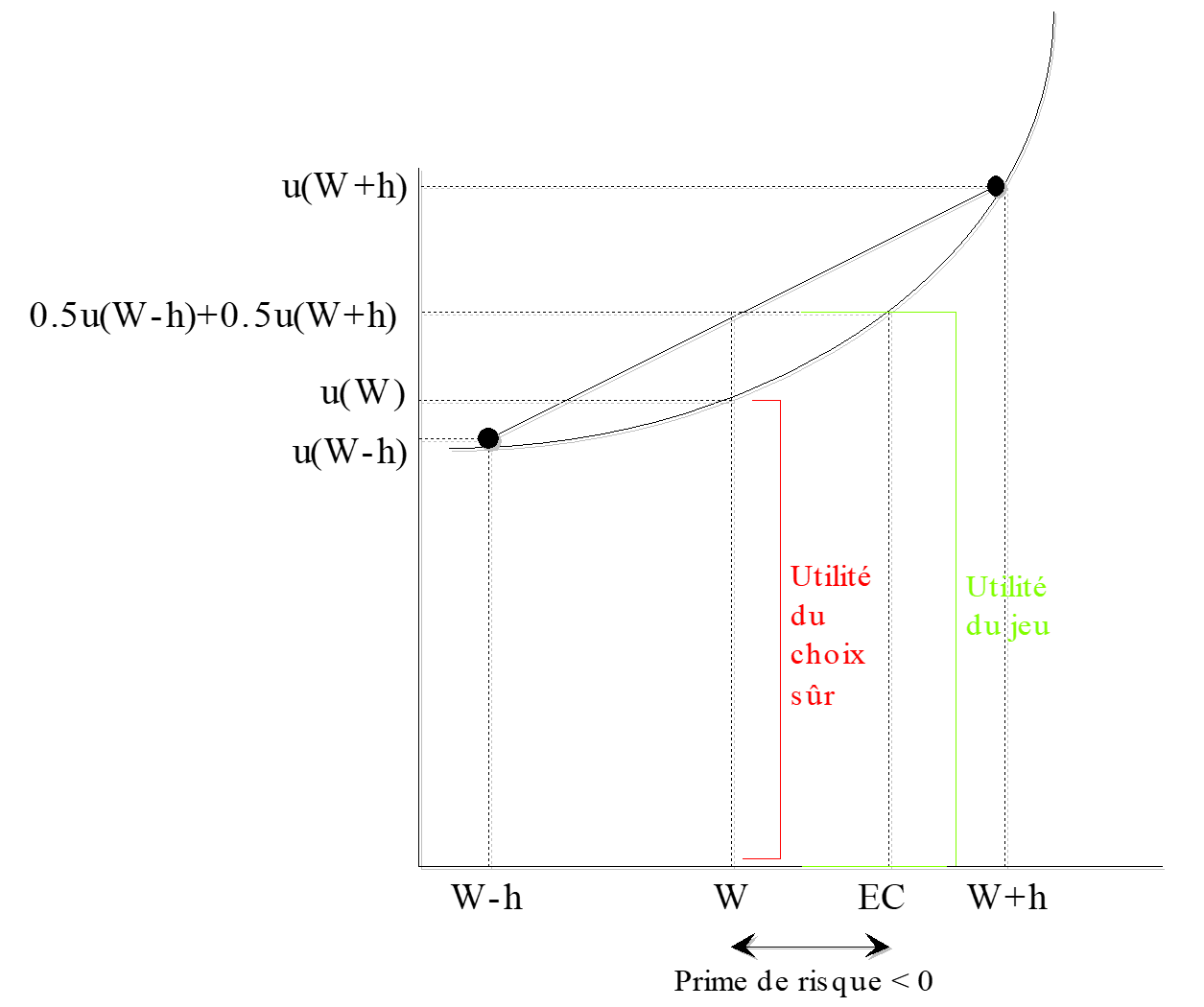
Figure 13.6: Représentation de la fonction d’utilité d’un individu aimant le risque.

Encadré 2 : Quand le goût du risque a réussi à RCA

Source : Shapiro C. et Varian H. (1999), Economie de l’information, De Boeck, coll. Balises, Paris, Bruxelles.

Le 1er juillet 1941, la télévision en noir et blanc fait son entrée aux Etats-Unis. RCA, propriétaire de NBC, était le principal fabricant. Tout au long des années 40, CBS, le plus grand réseau de télévision, fit pression pour que son système de télévision couleur soit adopté. Mais, ce système n’était pas compatible avec les téléviseurs existants. En octobre 1950, le standard CBS est accepté. RCA développe alors une stratégie agressive : augmenter la vente de téléviseurs en noir et blanc afin de renforcer l’incompatibilité du système CBS. Sur les 12 millions de télévisions américaines de l’époque, seules quelques douzaines pouvaient recevoir le système couleur de CBS. Et en 1953, 23 millions de téléviseurs en noir et blanc étaient installés. CBS jeta l’éponge en reconnaissant que le problème de la compatibilité était essentiel.

Le concept de prime de risque

Nous avons calculé dans les trois configurations, la prime de risque associée à la loterie. Pour un individu averse au risque, la prime de risque est positive. Celle d’un individu neutre au risque est nulle et celle d’un individu aimant le risque est négative.

Par exemple, si l’on reprend le titre financier qui peut rapporter 1000 dollars avec une probabilité ${^1/_4}$ ou 100 dollars avec une probabilité ${^3/_4}$. L’espérance de gain = 325 Francs. L’équivalent certain égale 178. La prime de risque $\Pi = 325 – 178 = 47 ~\text{dollars} > 0$. La fonction est une fonction concave et on retrouve bien une prime de risque positive.

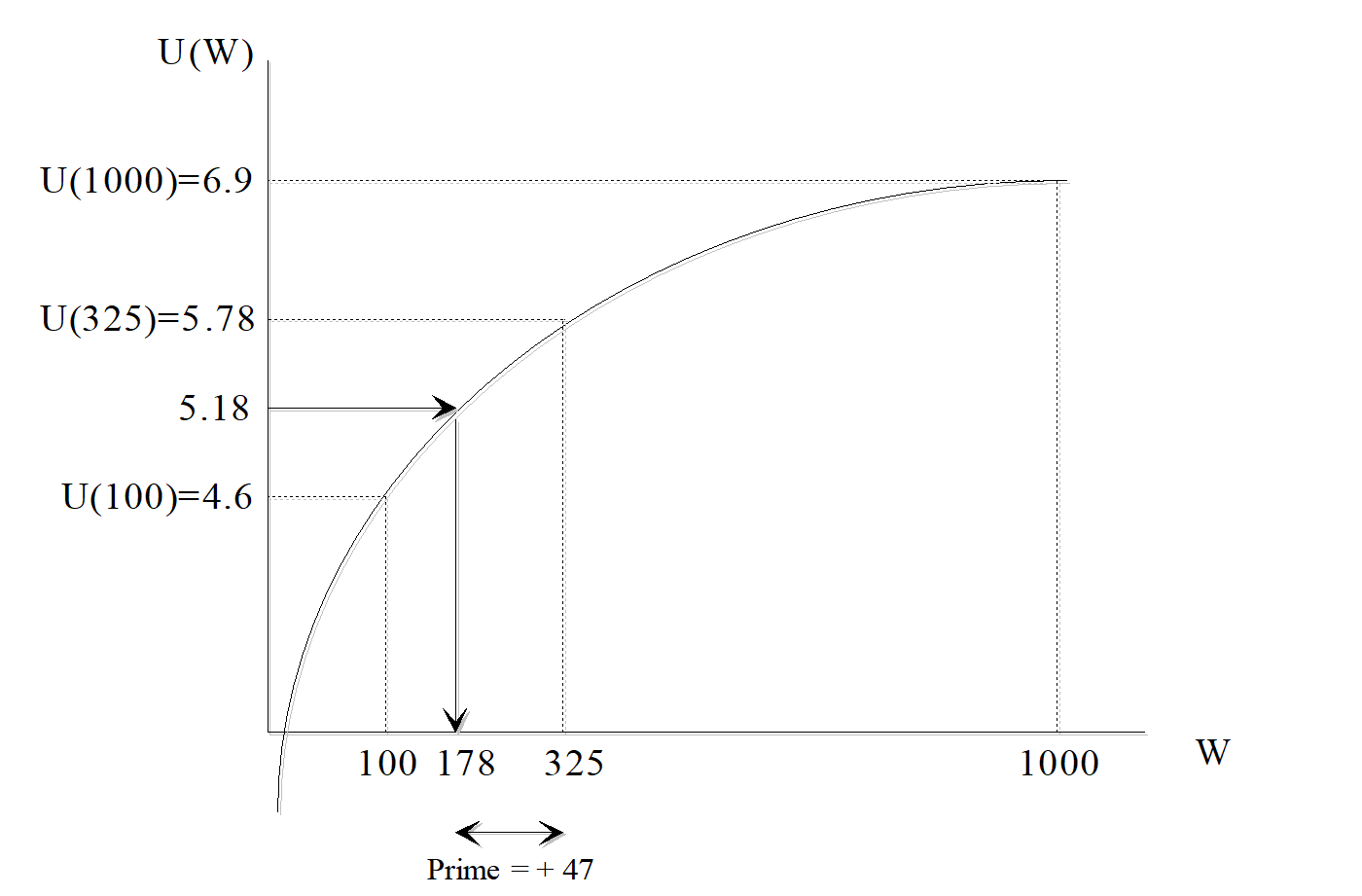
Figure 13.7: Fonction d’utilité concave et prime de risque.

Ce concept de prime de risque est fondamental pour expliquer le transfert de risque à l’assurance. En effet, la prime de risque permet d’expliquer pourquoi les individus supportent des primes d’assurance supérieures à la valeur actuarielle d’un risque¹³⁷.

Exemple Soit un chef d’entreprise exposé au risque d’incendie. Prenons le cas simple où il est confronté à une loterie binaire : soit l’incendie a lieu avec une probabilité 0,2 et détruit ses stocks d’une valeur de 500 000 $, soit il ne se passe rien avec une probabilité 0,8. La loterie associée à cette situation risquée est donc : $(0, 0.8 ; -500 000, 0.2)$. L’espérance de perte est de 10 000 $ et la valeur espérée des stocks est de 490 000 $. Mais si l’entrepreneur est averse au risque, il va préférer une somme certaine (même inférieure à 490 000 $) à la loterie qui peut détruire tous ses stocks et lui faire perdre 500 000 $. Ainsi si l’individu préfère 470 000 $ avec certitude, cela veut dire qu’il est prêt à perdre 20 000 $ pour se débarrasser du risque. Ces 20 000 $ représentent sa prime de risque. Ainsi, si un assureur lui propose une prime d’assurance inférieure à 20 000 $ pour couvrir le risque, il acceptera le transfert de risque vers l’assureur. L’assureur quand à lui recevra la prime de 20 000 $ pour un contrat dont le coût actuariel est de 10 000 $. Il acceptera donc de couvrir le risque.

L’écart entre l’espérance mathématique et l’équivalent certain de la loterie est donc une caractéristique propre à l’individu, son « prix du risque ». Le montant de la prime de risque exprimé en dollars, fournit une mesure acceptable de l’aversion au risque. De plus, on peut comparer les comportements des individus : on dira qu’un agent $A$ est moins risquophobe qu’un agent $B$, si face à la même loterie, $B$ accepte toujours de payer une prime de risque supérieure à celle de $A$, quelle que soit la loterie initiale.

13.2.4 Les critiques de l’utilité espérée : le paradoxe d’Allais (1954)

Le modèle de l’utilité espérée repose sur une base axiomatique qui implique que le critère de décision représentant le système de préférence du décideur est celui de l’espérance mathématique d’utilité. Cette hypothèse permet de relier le « prix du risque » à la forme de la fonction d’utilité et à la variance des pertes possibles. La spécificité de la fonction d’utilité permet de traduire d’une part, l’évaluation marginale des conséquences par le décideur et, d’autre part, de traduire son attitude par rapport au risque. L’utilité espérée a servi de pierre angulaire à la formation d’une nouvelle école, balayant le critère de l’espérance mathématique. Une axiomatique a été construite sur la base des travaux de Von Neumann et Morgenstern (1944). La théorie de l’espérance d’utilité et la théorie des probabilités subjectives répondent aux critères de la rationalité. Mais la littérature récente est également venue fragilisée cette axiomatique en lui opposant des paradoxes. En effet, le comportement réel des individus paraît violer certains axiomes. Un exemple célèbre est le paradoxe d’Allais (1953).

13.2.4.1 Mise en évidence du paradoxe

L’expérience d’Allais (1953) met en évidence une violation de l’axiome d’indépendance. Considérons l’exemple suivant. Un décideur doit choisir entre des loteries et on lui pose les deux questions suivantes :

Préférez-vous la situation A à la situation B ?

Option A + gain de 100 millions de dollars avec certitude
Option B + gain de 500 millions de dollars avec une probabilité de 0.1 + gain de 100 millions avec une probabilité de 0.89 + gain nul avec une probabilité de 0.01

Préférez-vous la situation C à la situation D ?

*C : + gain de 100 millions de dollars avec une probabilité 0.11 + gain nul avec une probabilité 0.89

*D : + gain de 500 millions de dollars avec une probabilité de 0.1 + gain nul avec une probabilité de 0.90

D’après l’expérience de 1953, 46 % des personnes qui répondent aux questions préfèrent A à B et D à C. Or ces choix sont incompatibles avec les axiomes de la théorie de l’utilité espérée. En effet, une telle configuration des préférences viole la linéarité en probabilité :

\[\begin{equation} A \succ B \iff U(100)>0.1U(500)+0.89U(100)\iff 0.11U(100)>0.1U(500)\iff C \succ D \end{equation}\]

L’origine exacte de cette violation est expliquée par Kahneman et Tversky (???) expliquent ce paradoxe par l’effet de certitude (appelé « effet de sécurité » par Allais (1953)). Cet effet reflète l’idée selon laquelle les individus ont tendance à surévaluer les résultats qui sont certains par rapport à des résultats qui ne sont que probables. Contrairement à ce que postule la théorie de l’utilité espérée, cet effet laisse supposer que les croyances, c’est à dire les probabilités, ne sont pas neutres. Si une personne a un tel comportement, c’est en fait qu’elle est attirée par la certitude : elle consent à une diminution de son espérance de gain pour aboutir à la certitude.

13.2.4.2 Explications du paradoxe d’Allais

Depuis le paradoxe d’Allais, de nombreux travaux de recherche ont cherché à reproduire, développer et généraliser ce type de contradiction. Afin d’interpréter ce paradoxe, Kahneman et Tversky (1979) invoquent la surpondération des faibles probabilités¹³⁸. Ainsi, cette transformation subjective des probabilités objectives suscite un effet de désir dans le domaine des gains et un effet inverse dans le domaine des pertes. Kahneman et Tversky (1979) mettent en évidence un effet de réflexion. Les préférences observées dans le domaine des gains s’inversent dans le domaine des pertes, comme le montre l’expérience qui suit :

Quelle situation préférez-vous ?	Quelle situation préférez-vous ?
A_1 : gain de 3000 avec une probabilité de 0.002	A_2 : perte de 3000 avec une probabilité 0.002
B_1 : gain de 6000 avec une probabilité de 0.001	B_2 : perte de 6000 avec une probabilité de 0.001
73 % des sujets préfèrent (B_1) à (A_1)	70% des sujets préfèrent (A_2) à (B_2)

Toutefois, nous restons prudents sur la symétrie car dans certains cas elle n’est pas parfaite.

D’autres phénomènes ont été mis en évidence de façon expérimentale¹³⁹ . Par exemple, les individus modifient leurs choix selon le référentiel utilisé pour spécifier les conséquences d’une perspective aléatoire. On parle ici d’effet de contexte (Tversky et Kahneman (1986)). Cet effet infirme l’hypothèse d’invariance des préférences par rapport au contexte de choix en mettant en évidence le rôle de la perception et des croyances dans le processus d’évaluation.

Exemple Un grand nombre de médecins ont été interrogés pour répondre au problème suivant :

Vous êtes médecin et vous occupez un poste de décision élevé au gouvernement. Vous venez d’apprendre qu’une nouvelle épidémie de grippe va frapper votre pays l’hiver prochain. Celle-ci pourrait entraîner la mort de 600 personnes. Les deux issues possibles lorsqu’un individu tombe malade sont la mort ou la guérison totale. Il existe deux types de programmes de prévention par vaccination. Le choix de l’un exclut le choix de l’autre. Le premier programme permet de sauver 200 personnes. Le second programme ne sauve personne avec une probabilité de $^2/_3$ et permet de sauver 600 personnes avec une probabilité de $^2/_3$. Quel programme de prévention choisissez vous ?

$\implies$ La majorité des médecins optent pour le refus du risque et choisissent le premier programme

Puis le même problème est soumis à un autre groupe mais avec une formulation différente :

Vous êtes médecin et vous occupez un poste de décision élevé au gouvernement. Vous venez d’apprendre qu’une nouvelle épidémie de grippe va frapper votre pays l’hiver prochain. Il existe deux types de programmes de prévention par vaccination. Le choix de l’un exclut le choix de l’autre. Avec le premier programme conduit à la mort de 400 personnes. Avec le second programme, il a $^1/_3$ de chances pour que personne ne meure, et $^2/_3$ de chance pour que les 600 meurent. Quel programme de prévention choisissez-vous ?

$\implies$ Dans ce cas, la réponse majoritaire a été le choix du risque : la mort certaine de 400 personnes est moins acceptable qu’une probabilité $^2/_3$ de «voir» mourir 600 personnes.

Les deux réponses données à ces problèmes ont été différentes On peut remarquer que les problèmes ont des conséquences identiques. Le contexte de choix affecte sans nul doute les appréciations comparatives des individus et leurs choix.

13.2.4.3 Le mimétisme

« Je sais calculer les mouvements des corps pesants, mais pas la folie des foules»¹⁴⁰, aurait déclaré Sir Isaac Newton , après avoir perdu des sommes considérables lors du Krach de la South Sea Company, en 1720. Une des explications : le comportement mimétique. En matière de choix stratégiques, le mimétisme est souvent la première stratégie à envisager. Pour bien le comprendre, il faut étudier les trois formes de mimétisme : normatif, informationnel et autoréférentiel. Le premier type correspond à la volonté d’être conforme aux normes sociales. Chaque individu recherche la reconnaissance du groupe. C’est le mimétisme normatif. Le deuxième type correspond au fait que nous pensons que les autres ont une information dont nous ne disposons pas. Ce mimétisme informationnel repose sur l’hypothèse d’asymétrie d’information de la théorie des jeux, dont nous verrons, dans le chapitre XX, les enjeux en matière organisationnelle. A titre d’exemple, si une entreprise invente un nouveau procédé de fabrication, le comportement mimétique sera de l’utiliser pensant que cette entreprise a de bonnes raisons de l’avoir développé, sans pour autant les connaître. Proche du mimétisme normatif, le troisième type intègre une dimension dynamique. Les agents vont faire leurs choix en fonction des choix des autres, non pas pour avoir une reconnaissance sociale, mais pour éviter de supporter certains coûts. Par exemple, les choix technologiques relèvent souvent du mimétisme autoréférentiel. Le choix du standard d’un ordinateur au moment de l’achat dépend du standard choisi par les personnes qui font partie de l’environnement de l’agent, car cela facilite l’échange des fichiers, etc. Ce mécanisme économique est connu également sous le nom de rétroactions positives¹⁴¹ dans la littérature.

Encadré 3 : Le concours de beauté de J.M. Keynes

Source :Keynes J.M. (1936), Théorie générale de l’emploi, de l’intérêt et de la monnaie¹⁴².

Le concours de beauté de John Maynard Keynes est devenu l’illustration type du mimétisme autoréférentiel. Les membres du concours doivent sélectionner le plus joli visage parmi une centaine de photographies ; le prix est attribué à celui dont la préférence s’approche le plus de la sélection moyenne réalisée par l’ensemble des concurrents. La bonne décision dépend du choix des autres.

La plupart de ces résultats empiriques qui vont à l’encontre de la théorie de l’utilité espérée, ont dans un premier temps été « expliqués » par un manque de rationalité de certains individus, une erreur de jugement voire une incompréhension des questions posées. Toutefois, tous ces comportements peuvent être expliqués si l’on élargit la conception de la rationalité au delà des axiomes de von Neumann et Morgenstern ou si l’on envisage des comportements de mimétisme. Ainsi, l’expérience d’Allais et celles qui ont suivi ont donné naissance à de nouvelles théories qui affaiblissent l’axiome d’indépendance et intègrent ainsi des comportements non explicables par la modélisation de von Neumann et Morgenstern. Ces nouvelles théories sont des généralisations de la théorie de l’utilité espérée.

13.3 Choix stratégiques en environnement incertain

Encadré 4 : Les consortiums, remède à l’incertitude ?

Le choix d’une nouvelle technologie par les consommateurs peut devenir un standard. Pour les entreprises développant des technologies différentes, l’incertitude règne. Philips en a fait les frais lorsqu’elle a lancé le DCC alors que Sony sortait son minidisc. Tous les événements possibles n’étaient pas connus (en matière de recherche et de développement, il est souvent difficile de connaître les stratégies des entreprises concurrentes) et les probabilités associées étaient impossibles à calculer. Une façon de se prémunir contre ce type de situation, dans des marchés sur lesquels les économies d’échelle peuvent être importantes, est le consortium. Avant d’investir lourdement dans la recherche et le développement de ce qui pourrait être un nouveau produit, il est intéressant de mobiliser quelques-uns des concurrents sur le même projet. Non seulement cela réduit les coûts d’investissement, mais cela a surtout l’avantage d’éviter que toute la concurrence ne lance des produits avec des standards différents. L’ensemble des événements possibles se resserre un peu, et l’incertitude se réduit. Les exemples de consortium sont nombreux : accords pour le disque laser, pour les mémoires de masse des ordinateurs, etc.

Dans la théorie des jeux, les équilibres en stratégies mixtes sont déterminés par l’utilisation de probabilités – expressions numériques de vraisemblances – dont la nature est exogène. Les joueurs essayent d’estimer la probabilité que leur concurrent choisisse une stratégie plutôt qu’une autre. Parfois, il est impossible d’avoir une connaissance sur les probabilités d’occurrence dans la mesure où la stratégie choisie par le concurrent dépend de facteurs multiples, complexes et pas tous connus au moment du choix. L’entreprise peut toutefois bien connaître son concurrent et avoir une idée subjective sur le comportement qu’il va adopter. Il effectuera son choix sur la base de cette estimation subjective. Nous allons tout d’abord présenter la théorie des probabilités subjectives de Savage (1954) puis nous présenterons l’environnement incertain au sens de Knight, c’est à dire non probabilisable. Même si les critères présentés supposent que l’ensemble des événements possibles est exhaustif, il ne faudra pas oublier que dans certains cas des événements peuvent être non anticipés ou non anticipables.

13.3.1 Les probabilités subjectives

D’une façon générale, lorsque les probabilités objectives sont inconnues, le décideur s’en remet à son estimation subjective de la vraisemblance de chaque résultat. Les individus placés en situation d’information imparfaite vont fonder leur comportement sur une estimation subjective des probabilités. Cette estimation peut varier en fonction des informations disponibles.

Exemple Un match de football rassemble tous ces éléments. Si l’on demande à un spectateur de dire quelle équipe sera gagnante, il s’appuiera sur des critères objectifs – l’état de fatigue des équipes, les individualités dans les équipes, etc. – et aussi sur des critères subjectifs – sa préférence pour l’une des deux équipes. Les probabilités qu’il attribuera aux différents événements possibles seront subjectives.

13.3.1.1 La théorie de Savage (1954)

L’élaboration classique de l’axiomatique des choix en situation d’incertitude subjective est due à Savage¹⁴³. Il considère qu’en l’absence de probabilité objective, les choix dépendent de la perception qu’un individu donné peut avoir de la vraisemblance de la réalisation d’un événement quelconque. L’individu va évaluer une situation incertaine comme s’il évaluait une décision risquée par rapport à des mesures de probabilité subjective. Savage s’est inspiré de l’axiomatique de Von Neuman et Morgenstern (1944) qui ont construit la pierre angulaire de la théorie de la décision : le concept d’utilité espérée, que nous avons étudié précédemment.

Nous allons essayer de comprendre comment se forment les probabilités subjectives. Chaque individu a des croyances qui lui permettent toujours d’assigner des probabilités subjectives aux différents états de la nature. Ces mesures de probabilité reflètent l’état d’esprit du décideur, son degré de conviction et d’information à l’égard de l’ensemble des éventualités.

Le cadre d’analyse de Savage (1954) est le suivant. Supposons qu’il existe un ensemble de résultats X et un ensemble d’états de la nature, $E$. Comme pour Knight (1921), l’ensemble des états est fini et connu. Chaque est une description de la résolution de toute l’incertitude. Les états de $E$ doivent être mutuellement exclusifs et exhaustifs. Si nous reprenons l’exemple du match de football, il y a trois issues possibles, notées respectivement $e1$, $e2$, et $e3$ : l’équipe 1 gagne, l’équipe 2 gagne ou les deux font match nul et $E$ est l’ensemble de tous les résultats possibles. Il faut ensuite former à partir de $X$ et de $E$, l’ensemble $L$ de toutes les loteries $l$. Par exemple, une loterie, $l$, décrit pour chaque état $e$, le résultat $x$ qui est gagné si $e$ est le résultat du match. Nous notons $l(e)$, le lot gagné à la loterie $l$ quand l’état de nature est $e$.

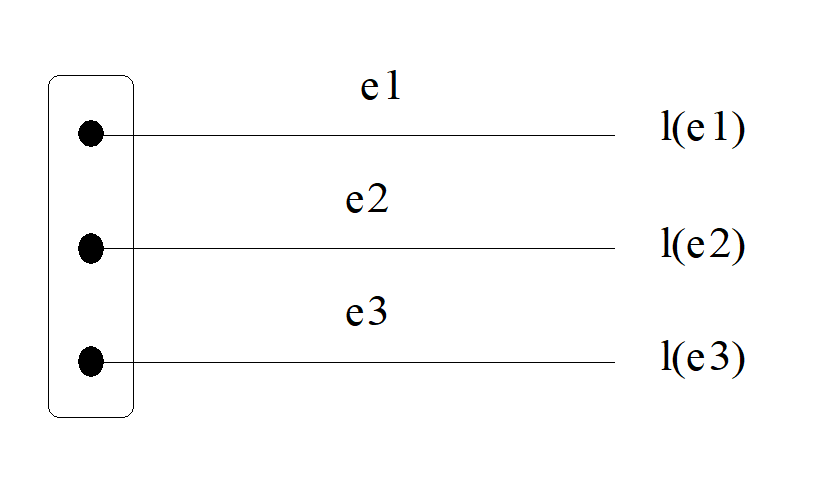
Figure 13.8: Représentation d’une loterie l.

Formellement, $L$ est l’ensemble de toutes les fonctions de $E$ dans $X$, soit . Dans la théorie de Savage, $L$ est l’ensemble des objets à choisir, les actions. Savage va attribuer une mesure à chacun des trois ensembles : les probabilités subjectives pour les états, l’utilité pour les résultats et l’espérance mathématique pour les actions. Il va élaborer 7 axiomes. Sans entrer dans le détail de la démarche de Savage, il peut être utile de présenter un axiome important : l’axiome d’indépendance (ou connu sous le nom de principe de la chose sûre).

Axiome d’indépendance de Savage Supposons que nous comparions deux loteries $l$ et $g$. Supposons de plus que l’ensemble $E$ des états de la nature contienne un sous-ensemble $S$ sur lequel $l$ et $g$ sont identiques : pour tout , $l(e)=g(e)$. Alors, la manière dont le consommateur apprécie $l$ par rapport à $g$ ne dépend que de la comparaison de $l$ et $g$ sur les états de la nature qui ne sont pas dans $S$.

En d’autres termes, l’individu estimera une probabilité subjective d’occurrence des deux loteries dans un état de nature en regardant ce que les deux loteries donnent dans les autres états de la nature. L’information qui l’intéresse est celle qu’il peut retirer de la réalisation des événements dans les autres états de la nature. La comparaison entre deux loteries est complètement indépendante de ce que valent ces loteries dans l’état de nature, $S$, dans lequel l’individu formera ses probabilités subjectives.

En termes de préférences, si un sujet préfère une loterie $l$ à une autre $g$ dans le cas où l’état de nature appartient à un sous-ensemble $S$, et préfère également $l$ à $g$ dans le complémentaire de $S$ ; alors il doit préférer $l$ à g même s’il ne sait pas si l’état de nature appartient à $S$ ou au complémentaire de S. Nous comprenons bien pourquoi cet axiome se nomme également « principe de la chose sûre ». En théorie des jeux, cela revient à avoir une stratégie dominante.

** Encadré 5 : Principe de la chose sûre et stratégie dominante : l’énigme de la toxine**

Source : Kavka G. (1983), « The Toxin Puzzle », Analysis, 43(1), janvier¹⁴⁴ .

Gregory Kavka met en évidence, dans un article de 1983, le lien entre l’axiome d’indépendance – ou le principe de la chose sûre – et la notion de stratégie dominante. Un milliardaire vous propose le marché suivant : « vous voyez cette fiole, elle contient une toxine qui, si vous l’absorbez, vous rendra malade comme un chien pendant deux jours, mais ne vous tuera pas et ne laissera aucune séquelle. Si vous avalez le contenu de la fiole, je vous verse un million de dollars. » Le marché semble facile et vous vous préparez à accepter quand votre interlocuteur ajoute : « ce qui m’intéresse n’est même pas que vous buviez la toxine ; il me suffit que vous en formiez l’intention demain à midi. Vous vous branchez ce soir à une machine qui mesure vos intentions. Si la machine a détecté une intention positive, vous trouverez le million de dollars sur votre compte. » Tout cela vous semble très bien parti. Mais, votre cerveau va vous trahir. Utilisons la théorie des jeux. Que vous ayez ou non trouvé le million de dollars sur votre compte, vous n’avez aucune raison de boire la toxine, et vous en avez une bonne de ne pas la boire. Il existe une stratégie dominante, ne pas boire, et c’est la stratégie rationnelle. Cela, vous le savez dès maintenant. Il vous est donc impossible de former l’intention de boire, sachant que vous savez qu’il n’est pas de votre intérêt de boire. Le million vous échappe.

13.3.1.2 L’apport d’Anscombe et Aumann (1963)

Savage (1954) part du principe de la chose sûre puis développe d’autres hypothèses plus complexes, qu’il est intéressant d’étudier. Toutefois, la formalisation mathématique utilisée est assez sophistiquée et dans la littérature¹⁴⁵ on présente souvent la formalisation plus simple utilisée par Anscombe et Aumann (1963)¹⁴⁶.

Anscombe et Aumann vont enrichir l’espace sur lequel sont définies les préférences. Pour cela, ils considèrent l’ensemble P des distributions de probabilité simple sur l’ensemble des résultats X. L’ensemble des événements E est fini. L est ici l’ensemble des fonctions de E dans P. Nous ne rentrerons pas dans le détail de l’axiomatisation pour ne pas compliquer inutilement notre propos.

Appliqué au match de football, cela signifie qu’ils introduisent de nouveaux éléments dans la description de la situation. Il s’agit de variables endogènes : par exemple, la possibilité de faire des changements de joueur. Toutefois, l’entraîneur déciderait de ces changements par un lancé de dé. La réalisation de la variable endogène suivrait donc une distribution de probabilité « objective ». Cela peut se représenter de la façon suivante :

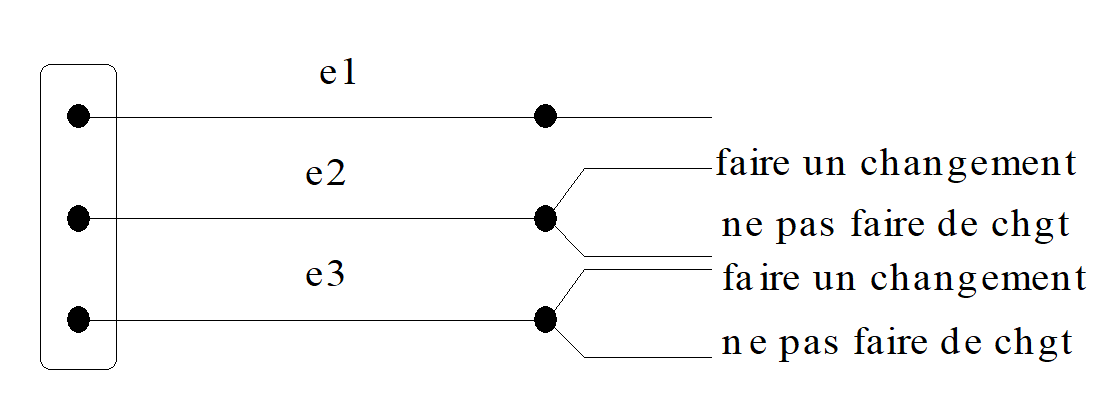
Figure 13.9: L’apport d’Anscombe et Aumann.

Anscombe et Aumann supposent que les individus ont des préférences sur ce nouvel ensemble L. Si l est la loterie définie « au sens élargi », l(./e) est l’élément de P qui est le résultat associé à la loterie dans l’état e et l(x/e) est la probabilité objective de gagner x sous l de manière contingente à l’état e. Dans une telle configuration, Anscombe et Aumann annoncent que la préférence d’un individu entre deux loteries élargies est indépendante de l’état dans lequel les deux loteries sont comparées. En d’autres termes, le consommateur évalue la probabilité subjective que le résultat du match soit e, et cela de façon indépendante de la réalisation de la loterie « changement ou pas de joueur ». Un pari sur le résultat du match est toujours estimé selon sa perception subjective. Ce résultat est proche de celui de Savage (1954).

En conclusion, un entrepreneur, au moment de décider d’une stratégie et s’il est en situation d’incertitude, formera des hypothèses sur une distribution de probabilité forcément subjective. Il intégrera également la possibilité que, peut-être, l’ensemble des états de la nature n’est pas exhaustif. À la probabilité subjective sur la réalisation d’un événement identifié, il ajoutera une probabilité subjective sur la possibilité que tous les événements n’aient pas été identifiés.

13.3.1.3 Le paradoxe d’Ellsberg (1961)

En l’absence d’informations sur les probabilités objectives, les probabilités peuvent être considérées comme « ambiguës ». Cette idée régénère l’idée de Knight (1921). En effet, le paradoxe d’Ellsberg met en lumière une aversion pour l’ambiguïté sur les probabilités de la part des décideurs et montre que les choix des individus ne respectent pas les axiomes de Savage. Reprenons l’expérience qui lui a permis d’arriver à ces conclusions.

Expérience

Soient deux urnes qui contiennent chacune des boules rouges et des boules noires. Une boule va être tirée au hasard dans l’une des urnes. Si l’individu interrogé pari sur la couleur rouge et qu’une boule rouge est tirée, il gagne $100 sinon il ne gagne rien, c’est à dire $0 (de la même façon pour les noires). Il possède les informations suivantes : dans l’urne 1, il y a 100 boules mais les proportions de chaque couleur sont inconnues (il peut y avoir de 0 à 100 boules rouges) alors que dans l’urne 2, il y en a exactement 50 de chaque.

Un observateur, qui ne connaît pas l’état de l’information sur les urnes, va essayer de mesurer les probabilités subjectives des individus en les interrogeant sur leurs préférences entre les situations suivantes :

Choix à l’intérieur des urnes :

Si l’on prend chacune des urnes indépendamment : « êtes-vous indifférents ou préférez-vous une couleur pour parier ? ». La plupart des individus sont indifférents, ce qui implique que les probabilités subjectives des deux événements sont égales à 0,5 : $p(R_1) = p(B_1)$ pour l’urne 1 et $p(R_2) = p(B_2)$ pour l’urne 2.

Choix entre les urnes :

Maintenant, si l’on demande de choisir entre les deux urnes pour parier sur la couleur rouge, les individus préfèrent l’urne 2. Ainsi, $p(R2)>p(R1)$. Pourtant, il se pourrait bien qu’il n’y ait que des boules rouges dans la première… ou 99 rouges et 1 noire… mais aussi que des noires. Les individus sont donc averses à l’ambiguïté. Si l’on demande pour la couleur noire, on a aussi $p(B2)>p(R2)$.

Ce qui montre qu’il y a une contradiction entre les probabilités qui reflètent les choix à l’intérieur de chaque urne et celles qui reflètent les choix entre les urnes. En effet, l’analyse des différents choix montre :

\[\begin{equation} p(R2)>p(R1)=0,5 ~\text{et } p(B2)>p(B1)=0,5 ~ \implies p(R2)+p(B2) >1 ~\implies ~\text{Sur-additivité} \\ \text{ou} p(R2) = 0,5 >p(R1) ~\text{et} p(B2) = 0,5 > p(B1) ~\implies p(R1) + p(B1)<1 ~\implies ~\text{Sous-additivité} \end{equation}\]

$\implies$ Ainsi dans chaque cas, les probabilités complémentaires ne sont pas additives. Ces choix sont incompatibles avec les propriétés essentielles des probabilités. Ainsi, dans un tel contexte, les choix ne révèlent pas des jugements sur les « probabilités ». Les axiomes de Savage et d’Anscombe-Aumann ne sont pas vérifiés.

La théorie des probabilités subjectives de Savage ne permet donc pas toujours de décrire les comportements des individus dans ce type de situation. Ellsberg (1961) explique que les individus sont averses à l’ambiguité. C’est pour cela que Kreps (1990) précise qu’il faut faire une réelle distinction entre les situations où il y a risque (probabilité objective) et les situations avec incertitude(probabilité subjective). De plus, ils n’aiment pas les situations dans lesquelles l’ensemble des événements peut être ouvert. Le fait de ne pas savoir à quel type d’ensemble d’événements ils sont confrontés (ouvert ou fermé) leur pose aussi un problème : les individus n’aiment pas l’éventualité de se tromper dans leurs évaluations des probabilités.

13.3.2 Choisir une stratégie en situation d’incertitude au sens de Knight

Nous allons considérer la vraisemblance ou la probabilité d’occurrence des différents états ne sont pas connues. Nous allons présenter les différents critères qui vont permettre de choisir une stratégie en situation de parfaite incertitude. R. Kast (1993)¹⁴⁷ dresse une liste de ces critères dont nous nous inspirons.

13.3.2.1 Le critère de Wald : le Maximin

L’individu va chercher à identifier la décision qui maximise le gain minimal. Il va définir pour chaque stratégie le résultat le plus défavorable et retenir celui offrant le moins défavorable. Ce critère est fortement pessimiste et correspond à un comportement de prudence extrême.

\[\begin{equation} W(d) = min {c_i(d) / i = 1,…,n} \end{equation}\]

On obtient donc pour les trois modes de production et pour les trois niveaux de concurrence $(i = 1,…,3) : W(C) = 10, W(I) = 4, W(S) = 5$. Le critère de Wald range donc les décisions dans l’ordre suivant : $C, S, I$. La décision optimale est le consortium.

13.3.2.2 Le Maximax

L’individu ne retient que le résultat le plus favorable de chaque décision d’investissement et choisit l’investissement maximisant ce résultat. Ce critère est fortement optimiste.

\[\begin{equation} M(d) = max {c_i(d) / i = 1,…,n} \end{equation}\]

On obtient donc : $M(C) = 30, M(I) = 30 et M(S) = 50$. Si l’individu applique ce critère, le classement est donc : $S, C et I$ donnant la même chose.

13.3.2.3 Le critère d’Hurwicz

Ce critère prend à la fois le meilleur et le pire résultat de chaque stratégie et les pondère dans une combinaison linéaire par un index de pessimisme k compris entre 0 et 1. La difficulté vient ici de la mesure du coefficient k. L’individu entreprend la stratégie qui lui donne le gain pondéré maximal.

\[\begin{equation} H(d) = k \times W(d) + (1-k) \times M(d) \end{equation}\]

Pour k = 1, on retrouve le critère de Wald et pour 0, le critère du Maximax. Si on choisit par exemple $k = 0,5$ (ni optimiste, ni pessimiste) on a : $H(C) = 0,5 \times 10 + (1-0,5) \times 30 = 20, H(I) = 17 et H(S) = 27,5$. Le classement est donc $S, C, I$.

13.3.2.4 Le critère de Savage : le minimax regret

Au lieu de ne considérer que les valeurs extrêmes, il est possible pour le décideur d’anticiper les « regrets » qu’il aurait en ayant pris une décision une fois que l’état de la nature est observé. Ces manques à gagner ($r$) sont calculés en faisant la différence entre le gain maximal qui aurait pu être obtenu en prenant une autre décision et le gain réalisé dans chaque état.

\[\begin{equation} S(d) = max {r_i(d) / i=1,…,n} \end{equation}\]

$S(C) = max {10-10, 25-20, 50-30 } = 20, ~S(I) = max {10-4, 25-25, 50-30 } = 20 ~\text{et}~ S(S) = max {10-5, 25-15, 50-50 } = 10$. Comme on cherche à minimiser le regret, dans ce cas le critère de Savage favorise $S$ et laisse les stratégies $C$ et $I$ indifférentes.

13.3.2.5 Le critère de Laplace : moyenne arithmétique des gains

Ce critère correspond à une pondération uniforme des différents états de la nature. En l’absence d’information sur les probabilités des événements élémentaires, l’individu les considère comme équiprobables.

\[\begin{equation} L(d)=\frac{1}{n}\sum_{i=1}^{n}c_i(d) \end{equation}\]

Pour $i = 1,…,3$, on pondère chaque résultat par $^1/_3$. $L(C) = 20,~L(I) = 59/3<20 ~\text{et}~ L(S) = 70/3>20$. Le critère de Laplace range donc les décisions dans l’ordre S, C et I. Ce critère se situe à la charnière de la distinction établie par Knight puisqu’il s’attache à convertir une situation incertaine en une situation risquée. On peut comparer les choix des différents critères :

Critères	Choix de la stratégie
Maximin	C, S, I
Maximax	S, C~I
Hurwicz	S, C, I
Savage	S, C~I
Laplace	S, C, I

Sur notre exemple extrêmement simple, comparé aux problèmes de stratégie et d’investissements réels , on voit que le choix d’un critère (qui dépend de la psychologie du décideur) peut modifier la décision finale, essentiellement si l’individu est optimiste. Le choix du mode de production dépend du caractère de l’entrepreneur en charge du choix de la stratégie : est-il optimiste, pessimiste, modéré ? En l’absence de visibilité sur l’avenir – ce qui est souvent le cas, à moins de travailler dans des univers déterministes – la décision repose sur des hypothèses comportementales plutôt que sur des estimations de vraisemblance. Toutefois, cette approche n’est pas éloignée de celle consistant à estimer des probabilités subjectives en l’absence de probabilités objectives. En effet, la comportement du décideur est modélisé en donnant une réalité quantitative à sa nature optimiste ou pessimiste.

Conclusion

Les critères de décision que nous avons énoncés tout au long du chapitre nous ont permis de mieux comprendre les décisions stratégiques prises dans un contexte d’incertitude. Bien que nous mettions l’accent sur l’utilisation de ces critères comme critères descriptifs de choix, ils sont également utilisés comme des guides normatifs pour des individus qui doivent faire des choix. L’économie expérimentale a beaucoup apporté à la théorie de la décision face au risque et à l’incertitude. Les paradoxes présentés dans ce chapitre sont tous apparus à l’occasion d’expérimentations en laboratoire. La démarche inductive, naturellement liée à cette branche de l’économie, essaye de faire ressortir les problèmes théoriques mais aussi d’apporter des éléments de réponse. Les théoriciens se sont intéressés à ces situations. Des développements récents ont permis de construire une théorie de l’utilité « non espérée »¹⁴⁸ , que nous laisserons ici de côté.

References

Allais, Maurice. 1953. “Le Comportement de L’Homme Rationnel Devant Le Risque. Critique Des Postulats et Axiomes de L’Ecole Américaine.” Econometrica 21 (October): 503–46.

Bernouilli, Daniel. 1738. “Specimen Theoriae Novae de Mensura Sortis.” Proceedings of the Imperial Academy 5: 175–92.

Bernstein, Peter L, and Juliette Hoffenberg. 1998. Plus Forts Que Les Dieux: [La Remarquable Histoire Du Risque. Paris: Flammarion.

Cramer, Gabriel. 1728. “Lettre à Nicolas Bernouilli.” Reproduite Dans Econometrica 22: 33–35.

Kahneman, Daniel, and Amos Tversky. 1979. “Prospect Theory: An Analysis of Decision Under Risk.” Econometrica 47: 263–92. http://links.jstor.org/sici?sici=0012-9682%28197903%2947%3A2%3C263%3APTAAOD%3E2.0.CO%3B2-3.

Knight, Frank Hyneman. 1921. Risk, Uncertainty and Profit. Boston: Houghton Mifflin Co.

Koenig, Christian. 1990. Management Stratégique, Paradoxes, Interactions et Apprentissages. Paris: Nathan.

Kreps, David M. 1990. A Course in Microeconomic Theory. Princeton, N.J.: Princeton University.

Loubergé, Henri. 1994. “L’incertitude, Dictionnaire de L’assurance.” Revue Risques 17.

Tversky, Amos, and Daniel Kahneman. 1986. “Rational Choice and the Framing of Decisions.” The Journal of Business 59: S251–S278. http://links.jstor.org/sici?sici=0021-9398%28198610%2959%3A4%3CS251%3ARCATFO%3E2.0.CO%3B2-C.

Von Neumann, John, and Oskar Morgenstern. 1944. Theory of Games and Economic Behavior. Princeton, Princeton university press.

p. 92.↩︎
p. 781, repris dans Kœnig (1990), p. 93.↩︎
Une définition du principe de précaution est donnée par la législation française (article 1, loi du 2 février 1995) : « l’absence de certitude, compte tenu des connaissances scientifiques du moment, ne doit pas retarder l’adoption de mesures effectives et proportionnées visant à prévenir un risque de dommages graves et irréversibles à un coût économiquement acceptable ». ↩︎
Pascal, (1654), La Géométrie du hasard.↩︎
Ce problème avait déjà été discuté par Montmort (1708)↩︎
Une situation peut correspondre à la loterie présentée précédemment ou à toute autre distribution de probabilité discrète ou continue↩︎
Ce qui permet aux compagnies d’assurance d’amortir leurs frais généraux et de dégager des profits.↩︎
Certains auteurs ont souligné l’effet inverse chez des assurés pour des pertes extrêmement rares. En effet, pour les catastrophes naturelles les individus refusent de s’assurer car ils sous-pondèrent la probabilité (et dans certains cas, ils la considèrent même comme nulle). ↩︎
Voir l’article de Munier et de Marcellis (1999)↩︎
In Orléan A. (1999), « L’imitation en finance est-elle efficace ? », Pour la Science, juillet, pp. 120-125.↩︎
Arthur B. (1989), « Competing Technologies, Increasing Returns and Lock-in by Historical Events », Economic Journal, 99(394), pp. 116-131, mars.↩︎
In Orléan A. (1999), « L’imitation en finance est-elle efficace ? », Pour la Science, juillet, pp. 120-125.↩︎
Savage L. (1954), The Foundations of Statistics, New York, John Wiley and Sons, Rev. And enl. Ed., New York, Dover Publications, 1972.↩︎
In Dupuy J.P. (1999), « Rationalité et irrationalité des choix individuels », Pour la Science, juillet, pp.68-73.↩︎
Voir Kreps (1990)↩︎
Anscombe F. et Aumann R. (1963) « A Definition of Subjective Probability », Annals of Mathematical Statistics, 34, pp. 199-205.↩︎
Kast R. (1993), La théorie de la décision, La Découverte, coll. Repères, Paris.↩︎
Pour une description des travaux récents généralisant la théorie de l’utilité espérée voir l’article de M. MACHINA (1982), « Expected Utility Analysis without the Independence Axiom », Econometrica, vol. 50, pp. 277-323.↩︎